题目内容
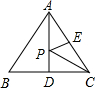 如图,已知点P是边长为2的正三角形ABC的中线AD上的动点,E是AC边的中点,则PC+PE的最小值是
如图,已知点P是边长为2的正三角形ABC的中线AD上的动点,E是AC边的中点,则PC+PE的最小值是| 3 |
| 3 |
分析:要求PE+PC的最小值,PE,PC不能直接求,可考虑通过作辅助线转化PE,PC的值,从而找出其最小值求解.
解答: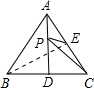 解:如下图所示:
解:如下图所示:
连接BE,
则BE就是PE+PC的最小值,
∵△ABC是一个边长为2的正三角形,AD为它的中线,点E是边AC的中点,
∴CE=1cm,
∴BE=
=
,
∴PE+PC的最小值是
.
故答案为:
.
 解:如下图所示:
解:如下图所示:连接BE,
则BE就是PE+PC的最小值,
∵△ABC是一个边长为2的正三角形,AD为它的中线,点E是边AC的中点,
∴CE=1cm,
∴BE=
| 22-12 |
| 3 |
∴PE+PC的最小值是
| 3 |
故答案为:
| 3 |
点评:考查等腰直角三角形的性质和轴对称及勾股定理等知识的综合应用,解题关键是对这些知识的熟练掌握及灵活运用,难度一般.

练习册系列答案
相关题目
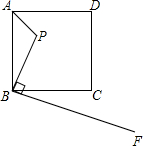 如图,已知点P是边长为5的正方形ABCD内一点,且PB=3,BF⊥BP于B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,BM的值为( )
如图,已知点P是边长为5的正方形ABCD内一点,且PB=3,BF⊥BP于B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,BM的值为( )| A、3 | ||
B、
| ||
C、3或
| ||
| D、3或5 |
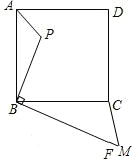 如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,若在射线BF有一点M,使以点B,M,C为顶点的三角形与△ABP相似,那么BM=
如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,若在射线BF有一点M,使以点B,M,C为顶点的三角形与△ABP相似,那么BM= 21、如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B.
21、如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B. 如图,已知点P是边长为5的正方形ABCD内的一点,连结PA,PB,PC,若PA=2,PB=4,∠APB=135°.
如图,已知点P是边长为5的正方形ABCD内的一点,连结PA,PB,PC,若PA=2,PB=4,∠APB=135°.