题目内容
【题目】小峰和同学探究一个问题:圆上的一点(不与已知直径端点重合)到圆直径两端点的距离与直径的数量关系.如图1,他们以![]() 为直径作了一个圆,圆心为
为直径作了一个圆,圆心为![]() ,在圆上取了三个不与点
,在圆上取了三个不与点![]() 重合的三点
重合的三点![]() ,连接
,连接![]() .
.




(1)通过观察,可猜想![]() 都是 三角形.请用图2中的
都是 三角形.请用图2中的![]() 来请证明你的猜想并写出
来请证明你的猜想并写出![]() 与
与![]() 的数量关系.
的数量关系.
(2)如图3,若![]() 且
且![]() 比
比![]() 少
少![]() ,求圆
,求圆![]() 的直径
的直径![]() 的长.
的长.
(3)如图4,动点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 出发,沿直径
出发,沿直径![]() 往点
往点![]() 运动,当运动到点
运动,当运动到点![]() 时停止在 (2)的条件下,当
时停止在 (2)的条件下,当![]() 秒时 ,
秒时 ,![]() 是等腰三角形.
是等腰三角形.
【答案】(1)直角;![]() ;(2)
;(2) ![]() ;(3) 6.25或
;(3) 6.25或![]() 或9
或9
【解析】
(1)利用等腰△OAC、等腰△OBC底角相等,以及三角形内角和,即可推出![]() ,即可得出结论;
,即可得出结论;
(2)运用勾股定理可得![]() 列出方程,求解,即可以得出答案;
列出方程,求解,即可以得出答案;
(3)分AP=AC,AP=CP,AC=CP三种情况讨论即可.
(1)直角
证明:如图,连接![]() .
.
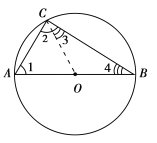
![]() 都是圆
都是圆![]() 的半径,
的半径,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() 为直角三角形,
为直角三角形,
![]() .
.
(2)由![]() 可知,
可知,![]() 为直角三角形,
为直角三角形,![]()
同理,![]() 为直角三角形,
为直角三角形,![]() .
.
由勾股定理,得![]() .
.
设![]() 为
为![]() ,则
,则![]() ,代入上式可得,
,代入上式可得,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]()
(3) 依题意得:AP=2t,AC=15
当AP=AC时,2t=15
解得:t=7.5
当AP=CP时,
∵OA=OC
∴P与O点重合
∴![]()
解得:t=6.25
当CP=AC=15时,如图:过C作CM⊥AB于M
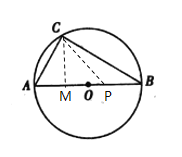
∵AB=25,AC=15,BC=20,∠ACB=90°
又∵![]()
∴![]()
∴![]()
在Rt△ACM中,![]()
∵AC=CP,CM⊥AB
∴AP=2AM=18
∴2t=18
∴t=9
综上所述:t的值:6.25或![]() 或
或![]() .
.
故答案为:6.25或![]() 或9
或9

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目






