题目内容
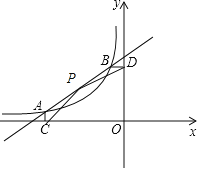
【题目】如图，已知A(﹣3，
)，B(﹣1，m)是一次函数y＝kx+b与反比例函数y＝
图象的两个交点，AC⊥x轴于点C，BD⊥y轴于点D．
（1）求m的值及一次函数解析式；
（2）P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标．
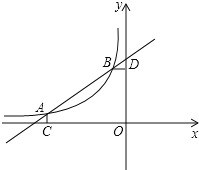
【答案】（1）2，y＝
x+
；（2）(﹣2，
)
【解析】
（1）把A点坐标代入反比例函数y＝
中求出n，得到n＝﹣2，则得到反比例函数解析式，然后利用反比例函数解析式确定B点坐标，然后利用待定系数法求一次函数解析式；
（2）连接PC、PD，如图，设P（x，x+），利用三角形面积公式得到
×（x+3）＝×|﹣1|×（2﹣x﹣），解方程求出x，从而得到P点坐标．
解：（1）∵反比例函数y＝的图象过点（﹣3，），
∴n＝﹣3×＝﹣2，
∵点B（﹣1，m）也在该反比例函数的图象上，
∴﹣1m＝﹣2，
∴m＝2；
把点A（﹣3，），B（﹣1，2）代入y＝kx+b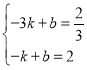得
，解得
，
∴一次函数的解析式为y＝x+；
（2）连接PC、PD，如图，设P（x，x+），
∵△PCA和△PDB面积相等，
∴×（x+3）＝×|﹣1|×（2﹣x﹣），
解得x＝﹣2，
当x＝﹣2时，y＝x+＝，
∴P点坐标是（﹣2，）．
【题目】某公司销售部有营业员20人，该公司为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励，为了确定一个适当的月销售目标，公司有关部门统计了这20人某月的销售量，如下表所示：
某公司20位营业员月销售目标统计表
月销售量/件数 | 1760 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 5 | 6 | 4 |
请根据以上提供的信息解答下列问题：
（1）求这个月中20位营业员的月销售量的平均数；
（2）为了提高大多数营业员积极性，公司将发放A，B，C三个等级的奖金（金额：
），如果你是管理者，从平均数，中位数，众数的角度进行分析，你将如何确定领取A，B，C级奖金各需达到的月销售量．
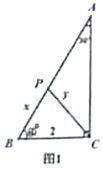
【题目】数学活动课上，小明同学根据学习函数的经验，对函数的图像、性质进行了探究，下面是小明同学探究过程，请补充完整：
如图1，已知在
，
，
，
，点
为
边上的一个动点，连接
．设
，
．
（初步感知）
（1）当
时，则①
________，②
________；
（深入思考）
（2）试求
与
之间的函数关系式并写出自变量的取值范围；
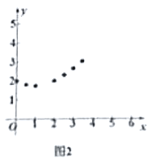
（3）通过取点测量，得到了与的几组值，如下表：
| 0 | 0.5 | 1 | 1.5 | 2. | 2.5 | 3 | 3.5 | 4 |
| 2 | 1.8 | 1.7 | _____ | 2 | 2.3 | 2.6 | 3.0 | _____ |
（说明：补全表格时相关数值保留一位小数）
1）建立平面直角坐标系，如图2，描出已补全后的表中各对应值为坐标的点，画出该函数的图象；
2）结合画出的函数图象，写出该函数的两条性质：
①________________________________；②________________________________．
