题目内容
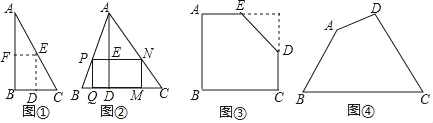
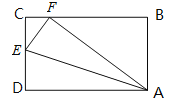
【题目】如图,正方形ABCD的边长为4,点E对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长为( )
A. 1B. 4-![]() C.
C. ![]() D.
D. ![]() -4
-4
【答案】B
【解析】
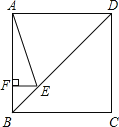
在AF上取FG=EF,连接GE,可得△EFG是等腰直角三角形,根据等腰直角三角形的性质可得EG=![]() EF,∠EGF=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAE+∠AEG=∠EGF,然后求出∠BAE=∠AEG=22.5°,根据等角对等边可得AG=EG,再根据正方形的对角线平分一组对角求出∠ABD=45°,然后求出△BEF是等腰直角三角形,根据等腰直角三角形的性质可得BF=EF,设EF=x,最后根据AB=AG+FG+BF列方程求解即可.
EF,∠EGF=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAE+∠AEG=∠EGF,然后求出∠BAE=∠AEG=22.5°,根据等角对等边可得AG=EG,再根据正方形的对角线平分一组对角求出∠ABD=45°,然后求出△BEF是等腰直角三角形,根据等腰直角三角形的性质可得BF=EF,设EF=x,最后根据AB=AG+FG+BF列方程求解即可.
解:如图,在AF上取FG=EF,连接GE,
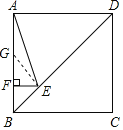
∵EF⊥AB,
∴△EFG是等腰直角三角形,
∴EG=![]() EF,∠EGF=45°,
EF,∠EGF=45°,
由三角形的外角性质得,∠BAE+∠AEG=∠EGF,
∵∠BAE=22.5°,∠EGF=45°,
∴∠BAE=∠AEG=22.5°,
∴AG=EG,
在正方形ABCD中,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴BF=EF,
设EF=x,∵AB=AG+FG+BF,
∴4=![]() x+x+x,
x+x+x,
解得x=2(2-![]() )=4-2
)=4-2![]() .
.
故选:B.

 备战中考寒假系列答案
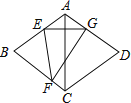
备战中考寒假系列答案【题目】如图,在菱形ABCD中,∠BAD=120°,点E,F分别在边AB,BC上,将菱形沿EF折叠,点B恰好落在AD边上的点G处,且EG⊥AC,若CD=8,则FG的长为( )
A. 6B. ![]() C. 8D.
C. 8D. ![]()
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,把超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:克) | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)若每袋食品的标准质量为450克,则抽样检测的20袋食品的总质量是多少克?
(2)若该种食品的合格标准为450±5克,求该种食品抽样检测的合格率?