ĢāÄæÄŚČŻ
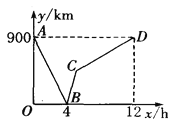
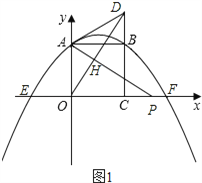
”¾ĢāÄæ”æČēĶ¼£ŗŅŃÖŖÕż·½ŠĪOABCµÄ±ßOC”¢OA·Ö±šŌŚxÖįŗĶyÖįµÄÕż°ėÖįÉĻ£¬µćB×ų±źĪŖ£Ø4£¬4£©£®¶ž“ĪŗÆŹż![]() µÄĶ¼Ļó¾¹żµćA”¢B£¬ĒŅÓėxÖįµÄ½»µćĪŖE”¢F£®µćPŌŚĻ߶ĪEFÉĻŌĖ¶Æ£¬¹żµćO×÷OH”ĶAPÓŚµćH£¬Ö±ĻßOH½»Ö±ĻßBCÓŚµćD£¬Į¬½ÓAD£®
µÄĶ¼Ļó¾¹żµćA”¢B£¬ĒŅÓėxÖįµÄ½»µćĪŖE”¢F£®µćPŌŚĻ߶ĪEFÉĻŌĖ¶Æ£¬¹żµćO×÷OH”ĶAPÓŚµćH£¬Ö±ĻßOH½»Ö±ĻßBCÓŚµćD£¬Į¬½ÓAD£®
£Ø1£©Ēób”¢cµÄÖµ£»
£Ø2£©ŌŚµćPŌĖ¶Æ¹ż³ĢÖŠ£¬µ±”÷AOPÓėŅŌA”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪĻąĖĘŹ±£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©ŌŚµćPŌĖ¶Æµ½OCÖŠµćŹ±£¬ÄÜ·ń½«”÷AOPČĘĘ½ĆęÄŚÄ³µćŠż×Ŗ90”ćŗóŹ¹µĆ”÷AOPµÄĮ½øö¶„µćĀäŌŚxÖįÉĻ·½µÄÅ×ĪļĻßÉĻ£æČōÄÜ£¬ĒėÖ±½ÓŠ“³öŠż×ŖÖŠŠÄMµÄ×ų±ź£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ£Ø1£©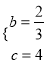 (2)P1£Ø2£¬0£©£»P2£Ø2+2
(2)P1£Ø2£¬0£©£»P2£Ø2+2![]() £¬0£©£»P3£Ø2©2
£¬0£©£»P3£Ø2©2![]() £¬0£©£®£Ø3£©£Ø2£¬2£©£¬£Ø1
£¬0£©£®£Ø3£©£Ø2£¬2£©£¬£Ø1![]() £¬3
£¬3![]() £©£¬£Ø©
£©£¬£Ø©![]() £¬
£¬ ![]() £©£»
£©£»
”¾½āĪö”æ£Ø1£©°Ń£Ø0£¬4£©£¬£Ø4£¬4£©·Ö±š“śČėy=©![]() x2+bx+cÖŠ£¬
x2+bx+cÖŠ£¬
µĆ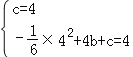 £¬
£¬
½āµĆ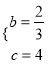 £»
£»
£Ø2£©½ā£ŗÉčP£Øt£¬0£©¢Łµ±PµćŌŚĻ߶ĪOCÉĻŹ±£¬ČēŌĶ¼ĖłŹ¾£»
”ß”ĻOAP£¼45”ć£¬”ĻBAD£¼45”ć
”ßČō”÷AOP”×”÷ABD£¬AO=AB£¬
”ąOP=BD£¬
”ąOP=BD=CD=2£¬
”ąt=2
”ąP1£Ø2£¬0£©£®
¢ŚµćPŌŚĻ߶ĪCFÉĻŹ±£¬ČēĶ¼1ĖłŹ¾£ŗ
”ß”ĻADB£¾”ĻODC£¬
”ß”ĻAPO=”ĻODC£¬
”ą”ĻABD£¾”ĻAPO£¬
”ąČō”÷AOP”×”÷ABD£¬Ōņ![]() =
=![]() £¬
£¬
ŌŚ”÷AOPÓė”÷OCDÖŠ
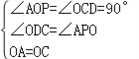
”ą”÷AOP”Õ”÷OCD£ØAAS£©£¬
”ąOP=CD£¬
”ąDB=PC=t©4£¬
”ą![]() £¬
£¬
½āµĆt=2©2![]() £ØÉįČ„£©»ņt=2+2
£ØÉįČ„£©»ņt=2+2![]() £¬
£¬
”ąP2£Ø2+2![]() £¬0£©£®
£¬0£©£®

¢ŪµćPŌŚĻ߶ĪOEÉĻŹ±£¬ČēĶ¼2ĖłŹ¾£»
”ß”ĻCOD+”ĻODC=90”ć£¬”ĻHOP+”ĻAPO=90”ć£¬”ĻCOD=”ĻHOP£¬
”ą”ĻODC=”ĻAPO£¬
”ß”ĻODC£¾”ĻADB£¬
”ą”ĻAPO£¾”ĻADB£¬
”ąČō”÷AOP”×”÷ABD£¬Ōņ![]() =
=![]() £¬
£¬
ŌŚ”÷AOPÓė”÷OCDÖŠ
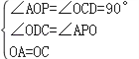
”ą”÷AOP”Õ”÷OCD£ØAAS£©£¬
”ąOP=CD£¬
”ąDB=PC=4©t£¬
”ą![]() £¬
£¬
½āµĆt=2+2![]() £ØÉįČ„£©»ņt=2©2
£ØÉįČ„£©»ņt=2©2![]() £¬
£¬
”ąP3£Ø2©2![]() £¬0£©£®
£¬0£©£®
£Ø3£©£Ø2£¬2£©£¬£Ø1![]() £¬3
£¬3![]() £©£¬£Ø©
£©£¬£Ø©![]() £¬
£¬ ![]() £©£»
£©£»
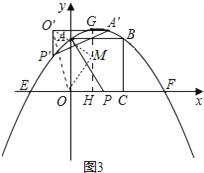
ČēĶ¼3ĖłŹ¾£ŗÉč”÷AOPČʵćMĖ³Ź±ÕėŠż×Ŗ90”ćµĆµ½”÷A”äO”äP”䣬ĒŅP”䔢A”äĮ½µćŌŚÅ×ĪļĻßy=©![]() x2+
x2+![]() x+4ÉĻ£¬
x+4ÉĻ£¬
ÉčO”ä£Øx£¬y£©£¬ŌņP”ä£Øx£¬y©2£©£¬A”ä£Øx+4£¬y£©
”ą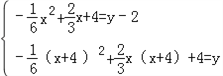 £¬
£¬
½āµĆ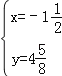 £¬
£¬
×÷MG”ĶO”äA”äÓŚG£¬MH”ĶOCÓŚH£¬ÉčM£Øa£¬b£©£¬
”ß”÷O”äMG”Õ”÷MOH£¬
”ąO”äG=MH=b£¬MG=OH=a£¬
”ą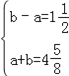 £¬
£¬
½āµĆ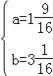 £¬
£¬
”ąM£Ø1![]() £¬3
£¬3![]() £©£®
£©£®

 Š”ѧʌĩ±ź×¼ŹŌ¾ķĻµĮŠ“š°ø
Š”ѧʌĩ±ź×¼ŹŌ¾ķĻµĮŠ“š°ø