题目内容
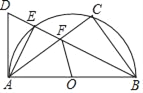
【题目】如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
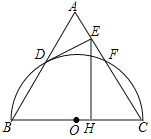
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)过点F作FH⊥BC,垂足为点H,若AB=4,求FH的长(结果保留根号).
【答案】1)DE是⊙O的切线;(2)![]() .
.
【解析】
试题(1)连接OD,根据等边三角形的性质得出AB=BC,∠B=∠C=60°,从而得出△OBD是等边三角形,∠BOD=∠C,再证OD∥AC,得出DE⊥OD,即可得出结论;
(2)先证明△OCF是等边三角形,得出CF=OC=2,再利用三角函数即可求出FH.
试题解析:(1)DE是⊙O的切线;理由如下:
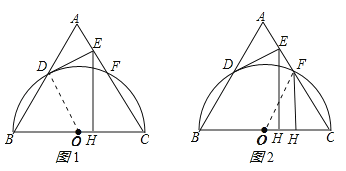
连接OD,如图1所示:∵△ABC是等边三角形,∴AB=BC=AC,∠B=∠C=60°,∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,∴∠BOD=∠C,∴OD∥AC,∵DE⊥AC,∴DE⊥OD,∴DE是⊙O的切线;
(2)连接OF,如图2所示:∵OC=OF,∠C=60°,∴△OCF是等边三角形,∴CF=OC=![]() BC=
BC=![]() AB=2,∵FH⊥BC,∴∠FHC=90°,∴FH=CFsin∠C=2×
AB=2,∵FH⊥BC,∴∠FHC=90°,∴FH=CFsin∠C=2×![]() =
=![]() .
.

练习册系列答案
相关题目