题目内容
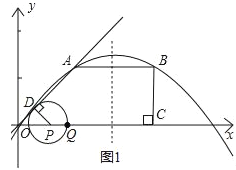
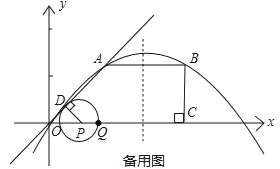
【题目】AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.
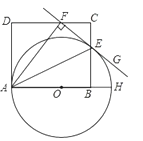
(1)求证:直线FG是⊙O的切线;
(2)若CD=10,EB=5,求⊙O的直径.
【答案】(1)见解析证明;(2)![]() .
.
【解析】试题分析:(1)连接OE,证明FG是⊙O的切线,只要证明∠OEF=90°即可;
(2)设OA=OE=x,则OB=10﹣x,在Rt△OBE中,∠OBE=90°,BE=5,由勾股定理列出方程,求出x的值,即可解答.
试题解析:(1)如图1,连接OE,∵OA=OE,∴∠EAO=∠AEO,∵AE平分∠FAH,∴∠EAO=∠FAE,∴∠FAE=∠AEO,∴AF∥OE,∴∠AFE+∠OEF=180°,∵AF⊥GF,∴∠AFE=∠OEF=90°,∴OE⊥GF,∵点E在圆上,OE是半径,∴GF是⊙O的切线;
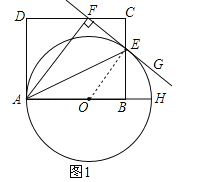
(2)∵四边形ABCD是矩形,CD=10,∴AB=CD=10,∠ABE=90°,设OA=OE=x,则OB=10﹣x,在Rt△OBE中,∠OBE=90°,BE=5,由勾股定理得:![]() ,∴
,∴![]() ,∴
,∴![]() ,∴AH=
,∴AH=![]() =
=![]() ,∴⊙O的直径为
,∴⊙O的直径为![]() .
.

【题目】某路公交车从起点出发,经过A、B、C三站到达终点,途中上下乘客如下表所示.(正数表示上车的人数,负数表示下车的人数)
上(下)车 | 起点 | A | B | C | 终点 |
上车的人数 | 10 | 9 | 6 | 5 | 0 |
下车的人数 | 0 | ﹣2 | ﹣5 | ﹣6 | ? |
(1)表格中“?”应填 .
(2)车行驶在哪两站之间时,车上的乘客最多? 站和 站;
(3)若每人乘坐一站需要买票1元,则该车出车一次能收入多少钱?要求写出计算过程.
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +8 |
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?