题目内容
【题目】如图，正方形ABCD中，点E为边BC的上一动点，作AF⊥DE交DE、DC分别于P、F点，连PC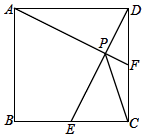
（1）若点E为BC的中点，求证：F点为DC的中点；
（2）若点E为BC的中点，PE=6，PC=4 
，求PF的长；
（3）若正方形边长为4，直接写出PC的最小值 ．
【答案】
（1）
证明：如图1中，
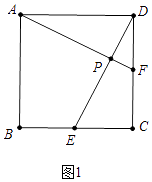
∵四边形ABCD是正方形，
∴AD=CD=BC，∠ADC=∠C=90°，
∵AF⊥DE，
∴∠APD=∠DPF=90°，
∴∠ADP+∠DAF=90°，∠ADP+∠EDC=90°，
∴∠DAF=∠EDC，
在△ADF和△DCE中，
，
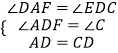∴△ADF≌DCE，
∴DF=CE，
∵EC= 
BC，BC=DC，
∴DF= DC，
∴F点为DC的中点；
（2）
解：如图1中，设PF=a，
易知△DPF∽△APD∽△ADF，
∴PF：DP=DP：AP=DF：AD=1：2，
∴DP=2a，AP=4a，AF=DE=5a，
∴PE=3a=6，
∴a=2，
∴PF=2．
（3）2 
﹣2
【解析】（3）解：如图2中，作△ADP的外接圆⊙H，连接CH，PH，EF．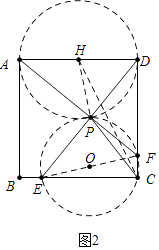
∵∠EPF=∠ECF=90°，
∴P、E、C、F在以EF为直径的⊙O上，
∵PH+PC≥CH，PH=2，CH= 
=2 ，
∴C、P、H共线时，PC的值最小，最小值为2 ﹣2．
所以答案是2 ﹣2．
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识，掌握全等三角形的对应边相等; 全等三角形的对应角相等，以及对正方形的性质的理解，了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
