题目内容
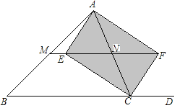
【题目】如图:在![]() 中,
中,![]() 、
、![]() 分别平分
分别平分![]() 与它的邻补角
与它的邻补角![]() ,
,
![]() 于
于![]() ,
,![]() 于
于![]() ,直线
,直线![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 试猜想
试猜想![]() 与
与![]() 的关系,并证明你的猜想;
的关系,并证明你的猜想;
![]() 如果四边形
如果四边形![]() 是菱形,试判断
是菱形,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)详见解析;(2)![]() 且
且![]() ,证明详见解析;(3)
,证明详见解析;(3)![]() 是直角三角形,证明详见解析.
是直角三角形,证明详见解析.
【解析】
(1)由AE⊥CE于E,AF⊥CF于F可得∠AEC=∠AFC=90°,再由,CE、CF分别平分∠ACB与它的邻补角∠ACD,能证出∠ECF=90°,从而得证.
(2)由矩形的性质可证NE=NC,从而可代换出内错角相等,两直线平行,又因为N是AC的中点,由三角形中位线定理相应的推论可知M是AB的中点.
(3)求出∠ACE=∠EAC=45°,求出AE=CE,根据菱形的判定推出即可.
![]() 证明:∵
证明:∵![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∴![]() ,
,
又∵![]() 、
、![]() 分别平分
分别平分![]() 与它的邻补角
与它的邻补角![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴三个角为直角的四边形![]() 为矩形;
为矩形;
(2)![]() 且
且![]() ;
;
证明:∵四边形![]() 为矩形,
为矩形,
∴对角线相等且互相平分,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() (矩形的对角线相等且互相平分),
(矩形的对角线相等且互相平分),
∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() ;
;
![]() 解:
解:![]() 是直角三角形
是直角三角形![]() ,
,
理由是:∵![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴四边形![]() 是菱形.
是菱形.

练习册系列答案
相关题目
【题目】(8分)在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:

请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有_____人;
(2)补全下表中空缺的三个统计量:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | 77.6 | 80 | _____ |
二班 | _____ | _____ | 90 |
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.






