Question

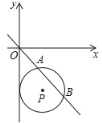
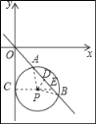
【题目】如图，在平面直角坐标系中，⊙P的圆心是（2，a），半径为2，直线y＝﹣x与⊙P相交于A、B两点，若弦AB的长为2，则a的值是（　　）

A. ﹣2B. ﹣2+C. ﹣2﹣D. ﹣2﹣

Answer 1

【答案】D

【解析】

设⊙P与y轴相切于点C，连接PC，则有PC⊥OC，根据点P的坐标可得⊙P的半径PC为2，连接CP并延长交直线y＝x于点E，则有CE＝OC．过点P作PD⊥AB于D，由垂径定理可求出AD，在Rt△ADP中，运用勾股定理可求出PD，在Rt△PDE中，运用三角函数可求出PE，就可求出a的值．

解：设⊙P与y轴相切于点C，连接PC，则有PC⊥OC．

∵点P的坐标为（2，a），

∴PC＝2．

①若点P在直线y＝x上方，如图1，

连接CP并延长交直线y＝x于点E，则有CE＝OC．

∵CE⊥OC，CE＝OC，

∴∠COE＝∠CEO＝45°．

过点P作PD⊥AB于D，

由垂径定理可得：AD＝BD＝AB＝．

在Rt△ADP中，

PD＝＝1．

在Rt△PDE中，

sin∠PED＝，

解得：PE＝．

∴OC＝CE＝CP+PE＝2+．

∴a＝﹣2﹣．