Question

已知函数y=|8-2x-x²|和y=kx+k（k为常数），则不论k为何值，这两个函数的图象

1. A.
   有且只有一个交点
2. B.
   有且只有二个交点
3. C.
   有且只有三个交点
4. D.
   有且只有四个交点

Answer 1

B
分析：首先画出二次函数的图象，一次函数与x轴一定经过点（-1，0）．根据图象即可确定交点的个数．
解答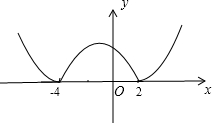：解：函数y=8-2x-x²中，令y=0，解得：x=-4或2．
则二次函数与x轴的交点坐标是（-4，0）和（2，0）．则函数的图象如图．
一次函数y=kx+k（k为常数）中，令y=0，解得：x=-1，故这个函数一定经过点（-1，0）．
经过（-1，0）的直线无论k多大，都是2个交点．
故选B．
点评：本题主要考查了一次函数与二次函数的图象，正确作出二次函数的答题图象，确定一次函数比经过（-1，0），利用数形结合思想是解题关键．