题目内容
 如图,已知在?ABCD中,E,F分别是AB,CD的中点,BD是对角线,AG∥DB交CB延长线于G.若四边形BEDF是菱形,则四边形AGBD是
如图,已知在?ABCD中,E,F分别是AB,CD的中点,BD是对角线,AG∥DB交CB延长线于G.若四边形BEDF是菱形,则四边形AGBD是
- A.平行四边形
- B.矩形
- C.菱形
- D.正方形
B
分析:先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD是矩形.
解答: 解:当四边形BEDF是菱形时,四边形AGBD是矩形.
解:当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形.
故选:B.
点评:主要考查了平行四边形、菱形的性质和矩形的判定.解题的关键是熟练掌握平行四边形、菱形性质以及矩形的判定定理.
分析:先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD是矩形.
解答:
 解:当四边形BEDF是菱形时,四边形AGBD是矩形.
解:当四边形BEDF是菱形时,四边形AGBD是矩形.证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形.
故选:B.
点评:主要考查了平行四边形、菱形的性质和矩形的判定.解题的关键是熟练掌握平行四边形、菱形性质以及矩形的判定定理.

练习册系列答案
相关题目
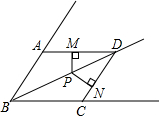 如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.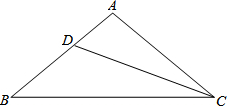 如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线.
如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线.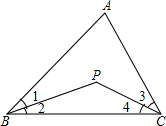 如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为
如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为 如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.
如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.