题目内容
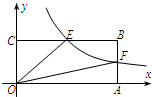 如图,已知双曲线y=
如图,已知双曲线y=| k | x |
分析:根据点F是AB的中点,设点F的坐标为(a,b),则点B的坐标是(a,2b),根据反比例函数的几何意义,△AOF与△COE的面积都等于
k,再利用矩形与△AOF与△COE的面积表示出四边形OEBF的面积,然后列式求解即可得到k值.
| 1 |
| 2 |
解答:解:∵点F是AB的中点,
∴设点F的坐标为(a,b),则点B的坐标是(a,2b),
∴S△AOF=S△COE=
ab=
k,
S矩形ABCO=a×2b=2ab=2k,
∴四边形OEBF的面积=S矩形ABCO-S△AOF-S△COE
=2k-
k-
k
=k
=6.
故答案为:6.
∴设点F的坐标为(a,b),则点B的坐标是(a,2b),
∴S△AOF=S△COE=
| 1 |
| 2 |
| 1 |
| 2 |
S矩形ABCO=a×2b=2ab=2k,
∴四边形OEBF的面积=S矩形ABCO-S△AOF-S△COE
=2k-
| 1 |
| 2 |
| 1 |
| 2 |
=k
=6.
故答案为:6.
点评:本题是反比例函数的综合考查,根据反比例函数图形的几何意义表示出三角形及四边形的面积是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
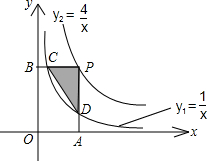 如图,已知双曲线
如图,已知双曲线 (2012•济南)如图,已知双曲线y=
(2012•济南)如图,已知双曲线y= (2013•徐州模拟)如图,已知双曲线y=
(2013•徐州模拟)如图,已知双曲线y= 如图,已知双曲线
如图,已知双曲线 如图,已知双曲线
如图,已知双曲线