题目内容
【题目】如图，所有正三角形的一边平行于x轴，一顶点在y轴上．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1、A2、A3、A4…表示，其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位，则顶点A3的坐标是 ， A92的坐标是 ．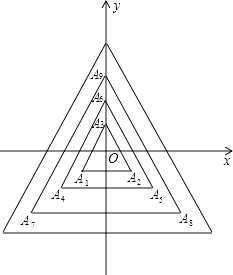 
【答案】（0， 
﹣1）；（31，﹣31）
【解析】解：∵△A1A2A3的边长为2，
∴△A1A2A3的高线为2× 
= ，
∵A1A2与x轴相距1个单位，
∴A3O= ﹣1，
∴A3的坐标是（0， ﹣1）；
∵92÷3=30…2，
∴A92是第31个等边三角形的第2个顶点，
第31个等边三角形边长为2×31=62，
∴点A92的横坐标为 
×62=31，
∵边A1A2与A4A5、A4A5与A7A8、…均相距一个单位，
∴点A92的纵坐标为﹣31，
∴点A92的坐标为（31，﹣31）．
故答案为：（0， ﹣1）；（31，﹣31）．
根据等边三角形的性质求出第一个三角形的高，然后求出A3O即可得解；
先根据每一个三角形有三个顶点确定出A92所在的三角形，再求出相应的三角形的边长以及A92的纵坐标的长度，即可得解．
【题目】某公司生产的某种商品每件成本为20元，经过市场调研发现，这种商品在未来40天内的日销售量m（件）与时间t（天）的关系如下表：
时间t（天） | 1 | 3 | 5 | 10 | 36 | … |
日销售量m（件） | 94 | 90 | 86 | 76 | 24 | … |
未来40天内，前20天每天的价格y1（元/件）与时间t（天）的函数关系式为y1= 
t+25（1≤t≤20且t为整数），后20天每天的价格y2（元/件）与时间t（天）的函数关系式为y2=﹣ 
t+40（21≤t≤40且t为整数）．
下面我们就来研究销售这种商品的有关问题：
（1）认真分析上表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m（件）与t（天）之间的表达式；
（2）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少？
