Question

在正方形ABCD中，点M是射线BC上一点，点N是CD延长线上一点，且BM=DN．直线BD与MN相交于E．
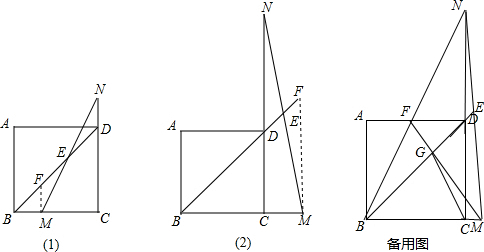
（1）如图1，当点M在BC上时，求证：BD－2DE=BM；
（2）如图2，当点M在BC延长线上时，BD、DE、BM之间满足的关系式是        ；
（3）在（2）的条件下，连接BN交AD于点F，连接MF交BD于点G．若DE=，且AF：FD=1：2时，求线段DG的长．

Answer 1

（1）证明见解析；（2）BD+2DE=BM；（3）．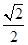

解析试题分析：（1）过点M作MF⊥BC交BD于点F，推出FM=DN，根据AAS证△EFM和△EDN全等，推出DE=EF，根据正方形的性质和勾股定理求出即可；
（2）过点M作MF⊥BC交BD于点F，推出FM=DN，根据AAS证△EFM和△EDN全等，推出DE=EF，根据正方形的性质和勾股定理求出即可；
（3）根据已知求出CM的长，证△ABF∽△DNF，得出比例式，代入后求出CD长，求出FM长即可．
试题解析：（1）过点M作MF⊥BC交BD于点F，
∵四边形ABCD是正方形，
∴∠C=90°，
∴FM∥CD，
∴∠NDE=∠MFE，
∴FM=BM，
∵BM=DN，
∴FM=DN，
在△EFM和△EDN中，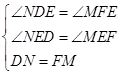
，
∴△EFM≌△EDN，
∴EF=ED，
∴BD-2DE=BF，
根据勾股定理得：BF=BM，
即BD-2DE=BM．
（2）过点M作MF⊥BC交BD于点F，与（1）证法类似：BD+2DE=BF=BM，
（3）由（2）知，BD+2DE=BM，BD=BC，
∵DE=，

∴CM=2，
∵AB∥CD，
∴△ABF∽△DNF，
∴AF：FD=AB：ND，
∵AF：FD=1：2，
∴AB：ND=1：2，
∴CD：ND=1：2，
CD：（CD+2）=1：2，
∴CD=2，∴FD=，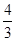
∴FD：BM=1：3，
∴DG：BG=1：3，
∴DG=．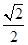
考点：1.正方形的性质；2.全等三角形的判定与性质；3.相似三角形的判定与性质．