题目内容
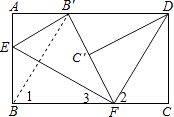
【题目】如图,将矩形纸片的两只直角分别沿EF、DF翻折,点B恰好落在AD边上的点B′处,点C恰好落在边B′F上.若AE=3,BE=5,则FC= . 
【答案】4
【解析】解:由题意得:B′E=BE=5,BF=B′F,∠BFE═∠EFB′,∠C′FD=∠DFC,
∴∠EFD=90°,
∴∠3+∠2=90°,
连接BB′,
∴EF⊥BB′,
∴∠1+∠3=90°,
∴∠1=∠2,
∵AE=3,四边形ABCD是矩形,
∴∠A=∠C=90°,AD∥BC,
∴∠AB′B=∠1,AB′= ![]() =4,
=4,
∴∠AB′B=∠2,
∵CD=AB=8,
在△ABB′与△CDF中,
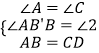 ,
,
∴△ABB′≌△CDF(AAS),
∴CF=AB′=4.
【考点精析】关于本题考查的勾股定理的概念和矩形的判定方法,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能得出正确答案.

练习册系列答案
相关题目