题目内容
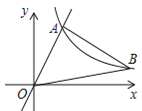
【题目】如图,已知AB为⊙O的直径,CD是弦,且AB![]() CD于点E。连接AC、OC、BC。
CD于点E。连接AC、OC、BC。
(1)求证: ![]() ACO=
ACO=![]() BCD。
BCD。
(2)若EB=![]() ,CD=
,CD=![]() ,求⊙O的直径。
,求⊙O的直径。

【答案】(1)详见解析;(2)⊙O的直径为26cm.
【解析】试题分析:(1)根据垂径定理可得CE=ED, ![]() ,由等弧所对的圆周角相等可得∠BCD=∠BAC,又因为△AOC是等腰三角形,即可得
,由等弧所对的圆周角相等可得∠BCD=∠BAC,又因为△AOC是等腰三角形,即可得![]() OAC=
OAC=![]() OCA,结论得证;(2)根据垂径定理可得CE=ED
OCA,结论得证;(2)根据垂径定理可得CE=ED![]() ,设⊙O的半径为Rcm,则OE= R
,设⊙O的半径为Rcm,则OE= R![]() 8,在Rt
8,在Rt![]() CEO中,根据勾股定理列出以R为未知数的方程,解方程即可求得圆的半径长,从而求得圆的直径的长.
CEO中,根据勾股定理列出以R为未知数的方程,解方程即可求得圆的半径长,从而求得圆的直径的长.
试题解析:
证明:(1)∵AB为⊙O的直径,CD是弦,且AB![]() CD于E,
CD于E,
∴CE=ED, ![]() ,
,
∴![]() BCD=
BCD=![]() BAC,
BAC,
∵OA=OC .
∴![]() OAC=
OAC=![]() OCA .
OCA .
∴![]() ACO=
ACO=![]() BCD .
BCD .
(2)设⊙O的半径为Rcm,则OE=OB![]() EB=R
EB=R![]() 8,
8,
CE=![]() CD=
CD=![]()
![]() 24=12,
24=12,
在Rt![]() CEO中,由勾股定理可得,
CEO中,由勾股定理可得,
OC![]() =OE
=OE![]() +CE
+CE![]() ,
,
即R![]() = (R
= (R![]() 8)
8) ![]() +12
+12![]() ,
,
解得 R=13.
∴2R=2![]() 13=26 .
13=26 .
答:⊙O的直径为26cm.

 寒假学与练系列答案
寒假学与练系列答案【题目】某校为提高学生的汉字书写能力,开展了“汉字听写”大赛.七、八年级学生参加比赛,为了解这两个年级参加比赛学生的成绩情况,从中各随机抽取10名学生的成绩,数据如下(单位:分):
七年级 88 94 90 94 84 94 99 94 99 100
八年级 84 93 88 94 93 98 93 98 97 99
整理数据:按如下分数段整理数据并补全表格:
成绩x 人数 年级 |
|
|
|
|
七年级 | 1 | 1 | 5 | 3 |
八年级 | 4 | 4 |
分析数据:补全下列表格中的统计量:
统计量 年级 | 平均数 | 中位数 | 众数 | 方差 |
七年级 | 93.6 | 94 | 24.2 | |
八年级 | 93.7 | 93 | 20.4 |
得出结论:你认为哪个年级学生“汉字听写”大赛的成绩比较好?并说明理由.(至少从两个不同的角度说明推断的合理性)
【题目】在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示.
成绩/ | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 |
则这些运动员成绩的中位数,众数分别为( )
A. 1.65,1.70 B. 1.65,1.75 C. 1.70,1.75 D. 1.70,1.70