题目内容
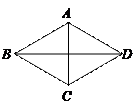
⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB=( )
| A.30° | B.45° | C.55° | D.60° |
B
连接OA,OB.根据正方形的性质,得∠AOB=90°再根据圆周角定理,即可求解.

解:连接OA,OB.根据正方形的性质,得∠AOB=90°.再根据圆周角定理,得∠APB=45°.
故选B.

解:连接OA,OB.根据正方形的性质,得∠AOB=90°.再根据圆周角定理,得∠APB=45°.
故选B.

练习册系列答案
相关题目
 、
、 的正方形纸片和
的正方形纸片和 的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次)在下面的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图的痕迹),使拼出的矩形面积为a2+3ab+2b2,并标出此矩形的长和宽.
的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次)在下面的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图的痕迹),使拼出的矩形面积为a2+3ab+2b2,并标出此矩形的长和宽.
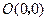 ,
,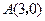 ,
,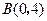 ,请你画出
,请你画出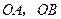 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形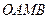 ;
;
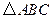 绕顶点
绕顶点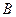 按顺时针方向旋转
按顺时针方向旋转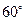 ,得到
,得到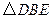 ,连结
,连结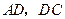 ,
,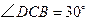 .求证:
.求证: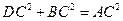 ,即四边形
,即四边形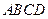 是勾股四边形
是勾股四边形
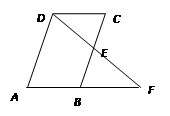




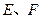 是
是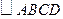 对角线
对角线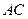 上的两点,且
上的两点,且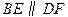 .
.
 ;
;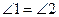 .
.
 -2
-2 -2
-2