题目内容
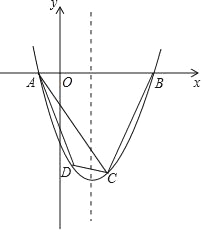
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c经过A、B、C三点,已知B(4,0),C(2,﹣6).
(1)求该抛物线的解析式和点A的坐标;
(2)点D(m,n)(﹣1<m<2)在抛物线图象上,当△ACD的面积为![]() 时,求点D的坐标;
时,求点D的坐标;
(3)在(2)的条件下,设抛物线的对称轴为l,点D关于l的对称点为E,能否在抛物线图象和l上分别找到点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形?若能,求出点P的坐标;若不能,请说明理由.
【答案】(1)点A的坐标(﹣1,0);(2)D(![]() ,
, ![]() ).(3)能.理由见解析
).(3)能.理由见解析
【解析】分析:(1)由B、C两点的坐标,利用待定系数法可求得抛物线的解析式,进而求出点A的坐标.(2)过D作DH垂直x轴于H,CG垂直x轴于G.则![]() ,进而求出D点坐标;(3)由D点坐标,可求得DE的长,当DE为边时,根据平行四边形的性质可得到PQ=DE=2,从而可求得P点坐标;当DE为对角线时,可知P点为抛物线的顶点,可求得P点坐标.
,进而求出D点坐标;(3)由D点坐标,可求得DE的长,当DE为边时,根据平行四边形的性质可得到PQ=DE=2,从而可求得P点坐标;当DE为对角线时,可知P点为抛物线的顶点,可求得P点坐标.
本题解析:
(1)∵抛物线y=x2+bx+c经过B、C二点,且B(4,0),C(2,﹣6),
∴![]() ,
,
解得:![]() ,
,
∴该抛物线的解析式:y=x2﹣3x﹣4,
∵抛物线y=x2﹣3x﹣4经过点A,且点A在x轴上
∴x2﹣3x﹣4=0,解得:x1=﹣1或x2=4(舍去)
∴点A的坐标(﹣1,0);
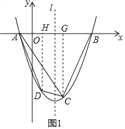
(2)如图1,过D作DH垂直x轴于H,CG垂直x轴于G.
∵点D(m,n)(﹣1<m<2),C(2,﹣6)
∴点H(m,0),点G(2,0).
则S△ACD=S△ADH+S四边形HDCG﹣S△ACG,
=![]() |n|(m+1)+
|n|(m+1)+![]() (|n|+6)(2﹣m)﹣
(|n|+6)(2﹣m)﹣![]() (|﹣1|+2)×|﹣6|
(|﹣1|+2)×|﹣6|
=![]() |n|﹣3m﹣3,
|n|﹣3m﹣3,
∵点D(m,n)在抛物线图象上,
∴n=m2﹣3m﹣4,
∵﹣1<m<2,即m2﹣3m﹣4<0
∴|n|=4+3m﹣m2,
∵△ACD的面积为:![]() ,
,
∴![]() (4+3m﹣m2)﹣3m﹣3=
(4+3m﹣m2)﹣3m﹣3=![]()
即4m2﹣4m+1=0,
解得m=![]() .
.
∴D(![]() ,
,![]() ).
).
(3)能.理由如下:
∵y=x2﹣3x﹣4=![]() ,
,
∴抛物线的对称轴l为![]() .
.
∵点D关于l的对称点为E,
∴E(![]() ,﹣
,﹣![]() ),∴DE=
),∴DE=![]() ﹣
﹣![]() =2.[来源:Z&xx&k.Com]
=2.[来源:Z&xx&k.Com]
①当DE为平行四边形的一条边时,如图2:
则PQ∥DE且PQ=DE=2.
∴点P的横坐标为![]() +2=
+2=![]() 或
或![]() ﹣2=﹣
﹣2=﹣![]() .
.
∴点P的纵坐标为(![]() ﹣
﹣![]() )2﹣
)2﹣![]() =﹣
=﹣![]() .
.
∴点P的坐标为(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ),
),
②当DE为平行四边形的一条对角线时,对角线PQ、DE互相平分,由于Q在抛物线对称轴上,对称轴l垂直平分DE,因此点P在对称轴与抛物线的交点上,即为抛物线顶点(![]() ,﹣
,﹣![]() ).
).
综上所述,存在点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形,点P的坐标为(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】前不久在台湾抗震救灾中,某地将甲、乙两个仓库的粮食全部转移到A、B两个仓库.甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A,B两库的路程和运费如下表:
路程(km) | 运费(元/吨km) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)函数关系式.
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?