题目内容
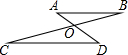 如图,AD与BC相交于点O,AB∥CD,如果∠B=15°,∠DOC=125°,那么∠D为( )
如图,AD与BC相交于点O,AB∥CD,如果∠B=15°,∠DOC=125°,那么∠D为( )分析:求出∠AOB,根据三角形内角和定理求出∠A,根据平行线性质得出∠D=∠A,代入求出即可.
解答:解:∵∠DOC=125°,
∴∠AOB=∠DOC=125°,
∵∠B=15°,
∴∠A=180°-∠AOB-∠B=40°,
∵AB∥CD,
∴∠D=∠A=40°,
故选B.
∴∠AOB=∠DOC=125°,
∵∠B=15°,
∴∠A=180°-∠AOB-∠B=40°,
∵AB∥CD,
∴∠D=∠A=40°,
故选B.
点评:本题考查了对顶角,三角形内角和定理和平行线的性质的应用,注意:两直线平行,内错角相等.

练习册系列答案
相关题目
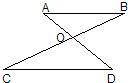 15、已知,如图,AD与BC相交于点O,AB∥CD,如果∠B=20°,∠D=40°,那么∠BOD为
15、已知,如图,AD与BC相交于点O,AB∥CD,如果∠B=20°,∠D=40°,那么∠BOD为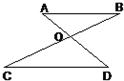 3、已知,如图:AD与BC相交于点O,AB∥CD,如果∠B=20°,∠D=40°,那么∠BOD为( )度.
3、已知,如图:AD与BC相交于点O,AB∥CD,如果∠B=20°,∠D=40°,那么∠BOD为( )度.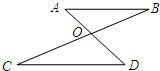 (2013•鹤壁二模)已知,如图,AD与BC相交于点O,AB∥CD,如果∠B=20°,∠D=40°,那么∠BOD为( )
(2013•鹤壁二模)已知,如图,AD与BC相交于点O,AB∥CD,如果∠B=20°,∠D=40°,那么∠BOD为( )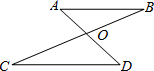 (2012•天桥区三模)已知,如图,AD与BC相交于点O,AB∥CD,如果∠B=20°,那么∠C为( )
(2012•天桥区三模)已知,如图,AD与BC相交于点O,AB∥CD,如果∠B=20°,那么∠C为( )