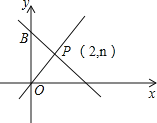Question

【题目】如图，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转，若∠BOA的两边分别与函数y=﹣、y=的图象交于B、A两点，则∠OAB的大小的变化趋势为（ ）

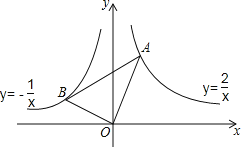
A．逐渐变小 B．逐渐变大 C．时大时小 D．保持不变

Answer 1

【答案】D

【解析】

试题分析：如图，作辅助线；首先证明△BOM∽△OAN，得到；设B（﹣m，），A（n，），得到BM=，AN=，OM=m，ON=n，进而得到mn=，mn=，此为解决问题的关键性结论；运用三角函数的定义证明知tan∠OAB=为定值，即可解决问题．

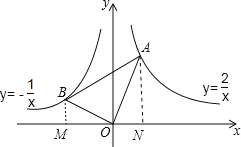
解：如图，分别过点A、B作AN⊥x轴、BM⊥x轴；

∵∠AOB=90°，

∴∠BOM+∠AON=∠AON+∠OAN=90°，

∴∠BOM=∠OAN，

∵∠BMO=∠ANO=90°，

∴△BOM∽△OAN，

∴；

设B（﹣m，），A（n，），

则BM=，AN=，OM=m，ON=n，

∴mn=，mn=；

∵∠AOB=90°，

∴tan∠OAB=①；

∵△BOM∽△OAN，

∴===②，

由①②知tan∠OAB=为定值，

∴∠OAB的大小不变，

故选：D．