题目内容
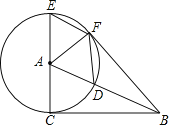
【题目】在等边![]() 中,点
中,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .试探索以下问题:
.试探索以下问题:
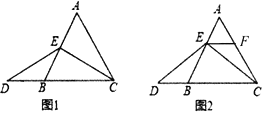
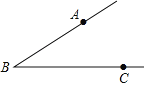
(1)当点![]() 为
为![]() 的中点时,如图1,求证:
的中点时,如图1,求证:![]() .
.
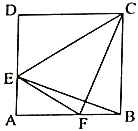
(2)如图2,当点![]() 不是
不是![]() 的中点时,过点
的中点时,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() 是等边三角形.
是等边三角形.
(3)在(2)的条件下,![]() 与
与![]() 还相等吗?请说明理由.
还相等吗?请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)ED=EC.
【解析】
(1)根据等边三角形的性质得出AB=AC=BC,∠ABC=∠ACB=∠A=60°,再由E是AB的中点,AE=BE=BD,证出∠EDB=∠ECB,得出EC=ED;
(2)在△AEF中,只要证明有两个内角是60°即可;
(3)只要证明△DBE≌△EFC,即可推出结论.
解:(1)证明:∵△ABC是等边三角形,
∴AB=AC=BC,
∠ABC=∠ACB=∠A=60o ,
∵E是AB的中点,
∴AE=BE,∠ECB=![]() ∠ACB=30°,
∠ACB=30°,
∵AE=BD,
∴BE=BD,
∴∠EDB=∠DEB=![]() ∠ABC=30°,
∠ABC=30°,
∴∠EDB=∠ECB,
∴EC=ED.
(2)∵EF∥BC,
∴∠AEF=∠ABC=60 o,∠AFE=∠ACB=60°,
∴△AEF是等边三角形,
(3)ED=EC.理由如下:
由(2)得:△AEF是等边三角形
∴∠AFE=∠ABC=60°,AE=EF=AF
∴∠EFC=∠DBE=120°,
又∵AE=BD,AB=AC,
∴BD=EF,BE=FC,
∴△DBE≌△EFC(SAS),
∴ED=EC.

 53随堂测系列答案
53随堂测系列答案【题目】某路公交车从起点经过A、B、C、D站到达终点,一路上下乘客如下表所示。(用正数表示上车的人数,负数表示下车的人数)
| 起点 | A | B | C | D | 终点 |
上车的人数 | 18 | 15 | 12 | 7 | 5 | 0 |
下车的人数 | 0 | -3 | -4 | -10 | -11 |
(1)到终点下车还有_________ 人;
(2)车行驶在那两站之间车上的乘客最多?_______站和________站;
(3)若每人乘坐一站需买票1元,问该车出车一次能收入多少钱?写出算式.