题目内容
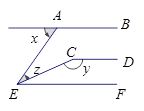
某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,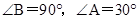 ;图②中,
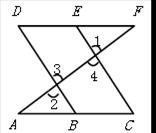
;图②中, .图③是该同学所做的一个实验:他将△
.图③是该同学所做的一个实验:他将△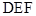 的直角边
的直角边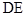 与△
与△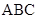 的斜边
的斜边 重合在一起,并将△
重合在一起,并将△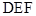 沿
沿 方向移动.在移动过程中,
方向移动.在移动过程中,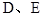 两点始终在
两点始终在 边上(移动开始时点
边上(移动开始时点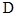 与点
与点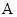 重合).
重合).
(1) 在△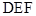 沿
沿 方向移动的过程中,该同学发现:
方向移动的过程中,该同学发现: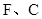 两点间的距离 ;连接
两点间的距离 ;连接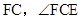 的度数 .(填“不变”、“ 逐渐变大”或“逐渐变小”)
的度数 .(填“不变”、“ 逐渐变大”或“逐渐变小”)
(2) △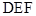 在移动过程中,
在移动过程中,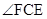 与
与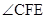 度数之和是否为定值,请加以说明;
度数之和是否为定值,请加以说明;
(3) 能否将△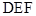 移动至某位置,使
移动至某位置,使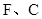 的连线与
的连线与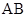 平行?如果能,请求出此时
平行?如果能,请求出此时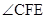 的度数,如果不能,请说明理由。
的度数,如果不能,请说明理由。
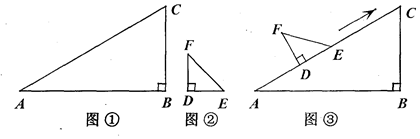
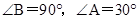 ;图②中,
;图②中, .图③是该同学所做的一个实验:他将△
.图③是该同学所做的一个实验:他将△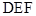 的直角边
的直角边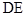 与△
与△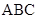 的斜边
的斜边 重合在一起,并将△
重合在一起,并将△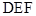 沿
沿 方向移动.在移动过程中,
方向移动.在移动过程中,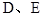 两点始终在
两点始终在 边上(移动开始时点
边上(移动开始时点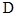 与点
与点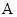 重合).
重合).(1) 在△
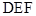 沿
沿 方向移动的过程中,该同学发现:
方向移动的过程中,该同学发现: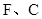 两点间的距离 ;连接
两点间的距离 ;连接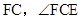 的度数 .(填“不变”、“ 逐渐变大”或“逐渐变小”)
的度数 .(填“不变”、“ 逐渐变大”或“逐渐变小”)(2) △
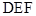 在移动过程中,
在移动过程中,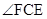 与
与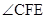 度数之和是否为定值,请加以说明;
度数之和是否为定值,请加以说明;(3) 能否将△
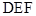 移动至某位置,使
移动至某位置,使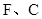 的连线与
的连线与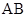 平行?如果能,请求出此时
平行?如果能,请求出此时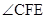 的度数,如果不能,请说明理由。
的度数,如果不能,请说明理由。
(1)变小,变大;(2)和为定值,理由见解析;(3)15°.
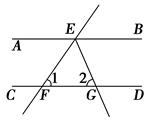
试题分析:(1)利用图形的变化得出F、C两点间的距离变化和,∠FCE的度数变化规律;
(2)利用外角的性质得出∠FEC+∠CFE=∠FED=45°,即可得出答案;
(3)要使FC∥AB,则需∠FCE=∠A=30°,进而得出∠CFE的度数.
试题解析:(1)F、C两点间的距离逐渐变小;连接FC,∠FCE的度数逐渐变大;
(2)∠FCE与∠CFE度数之和为定值;
理由:∵∠D=90°,∠DFE=45°,
又∵∠D+∠DFE+∠FED=180°,
∴∠FED=45°,
∵∠FED是△FEC的外角,
∴∠FEC+∠CFE=∠FED=45°,
即∠FCE与∠CFE度数之和为定值;
(3)要使FC∥AB,则需∠FCE=∠A=30°,
又∵∠CFE+∠FCE=45°,
∴∠CFE=45°-30°=15°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
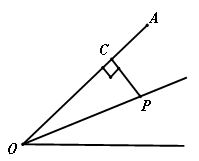


 a°, 则下列结论:
a°, 则下列结论:  (180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.
(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.
 ,∠BAC=60°,则AC= .
,∠BAC=60°,则AC= .
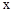 、∠
、∠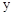 、∠
、∠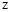 三者之间的关系是 .
三者之间的关系是 .