��Ŀ����
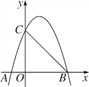
����Ŀ����ͼ��������y��ax2��bx��c��a��0����x�ᡢy��ֱ���A����1��0����B��3��0����C��0��3������.
��1�����������ߵĽ���ʽ��
��2��P��ֱ��BC�Ϸ����������ϵ�һ�����㣬��P�ĺ�����Ϊt��P��BC�ľ���Ϊh����h��t�ĺ�����ϵʽ�������h�����ֵ��
��3�����M��x���ϵĶ��㣬��ƽ��ֱ������ϵ�У��Ƿ���ڵ�N��ʹ���Ե�A��C��M��NΪ������ı��������Σ������ڣ�������з��������ĵ�N���ꣻ�������ڣ�˵������.
���𰸡�(1)y����x2��2x��3.(2) t��![]() ʱ�����ֵΪ
ʱ�����ֵΪ![]() .(3) ���ڣ�N1(0����3)��N2(��
.(3) ���ڣ�N1(0����3)��N2(��![]() ��3)��N3(
��3)��N3(![]() ��3)��N4(��5��3)��
��3)��N4(��5��3)��
�������������������1����A��B��C��������꣬���ô���ϵ��������������ߵĽ���ʽ��
��2������P��PD��x���ڵ�D����BC�ڵ�E��PH��BC�ڵ�H������PB��PC���������ֱ��BC�Ľ���ʽ�������t�ֱ��ʾ��E�����꣬�Ӷ��ɱ�ʾ��PE�ij����ٿ���t��ʾ����PBC������������õȻ�������t��ʾ��h�����ö��κ��������ʿ����h�����ֵ��
��3����AM��CM��ACΪ�Խ�������������ֱ�������ε����ʿ����N������꣮
�����������1����������y=ax2+bx+c��A��-1��0����B��3��0����C��0��3�����㣬
�� �����
����� ��
��
�������ߵĽ���ʽΪy=-x2+2x+3��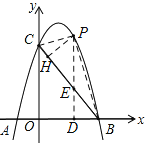
��2������P��PD��x���ڵ�D����BC�ڵ�E��PH��BC�ڵ�H������PB��PC��
��B��3��0����C��0��3����
��OB=OC=3��BC��![]() ��
��
��ֱ��BC����ʽΪy=kx+n����![]() �����
�����![]()
��ֱ��BC����ʽΪy=-x+3��
�ߵ�P�ĺ�����Ϊt������������y=-x2+2x+3�ϣ�
��P��t��-t2+2t+3����
�֡�PD��x���ڵ�D����BC�ڵ�E��
��D��t��0����E��t��-t+3����
��PE=��-t2+2t+3��-��-t+3��=-t2+3t��
��S��PBC��S��PEB+S��PEC��![]() PEBD+
PEBD+![]() PEOD��
PEOD��![]() PE(BD+OD)��
PE(BD+OD)��![]() PEOB=
PEOB=![]() (t2+3t)��3��
(t2+3t)��3��![]() t2+
t2+![]() t��
t��
�֡�S��PBC��![]() BCPH��
BCPH��![]() ��3
��3![]() h��
h��![]() h��
h��
��![]() h��
h��![]() t2+
t2+![]() t��
t��
��h��t�ĺ�����ϵʽΪ��h��![]() t2+
t2+![]() t��0��t��3����
t��0��t��3����
��h��![]() t2+
t2+![]() t��
t��![]() (t
(t![]() )2+
)2+![]() ��
��
�൱t��![]() ʱ��h�����ֵΪ
ʱ��h�����ֵΪ![]() ��
��
��3�����ڣ�
��AMΪ���ζԽ��ߣ���AM��CN���ഹֱƽ�֣�
��N��0��-3����
��CMΪ���ζԽ��ߣ���CN��AM��AC��![]() ��
��![]() ��
��
��N(![]() ��3)��N(
��3)��N(![]() ��3)��
��3)��
��ACΪ���ζԽ��ߣ���CN=AM=CM��
��M��m��0������CM2=AM2����m2+32=��m+1��2�����m=4��
��CN=AM=CM=5��
��N��-5��3����
���Ͽ�֪���ڵ�N��ʹ���Ե�A��C��M��NΪ������ı��������Σ����������ĵ�N��4����N1��0��-3����N2(![]() ��3)��N3(
��3)��N3(![]() ��3)��N4��-5��3����
��3)��N4��-5��3����

