题目内容
【题目】如图,已知AB∥CD,请分别判断下面四个图形中∠APC、∠PAB、∠PCD之间的关系.
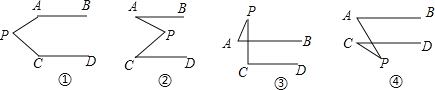
(1)写出相应的四个结论;
(2)请证明你所得的第③个图形的结论.
【答案】(1)①∠APC+∠PAB+∠PCD=360°,
②∠APC=∠PAB+∠PCD,
③∠APC=∠PCD﹣∠PAB,
④∠APC=∠PAB﹣∠PCD;
(2)见解析
【解析】
试题分析:分别过点P作PE∥AB,然后根据平行线的性质解答即可.
(1)解:①∠APC+∠PAB+∠PCD=360°,
②∠APC=∠PAB+∠PCD,
③∠APC=∠PCD﹣∠PAB,
④∠APC=∠PAB﹣∠PCD;
(2)证明:如图,过点P作PE∥AB,
∴∠APE=180°﹣∠PAB,
∵AB∥CD,
∴PE∥CD,
∴∠CPE=180°﹣∠PCD,
∴∠APC=∠APE﹣∠CPE=(180°﹣∠PAB)﹣(180°﹣∠PCD)=∠PCD﹣∠PAB.


练习册系列答案
相关题目