题目内容
观察下列一组式子的变形过程,然后回答问题:
=
-1,
=
-
,
=
-
,
=
-
…
(1)请你用含n(n为正整数)的关系式表示上述各式子的变形规律.并证明你的结论.
(2)利用上面的结论,求下列式子的值:(
+
+
+…+
)•(
+1).
| 1 | ||
|
| 2 |
| 1 | ||||
|
| 3 |
| 2 |
| 1 | ||||
|
| 4 |
| 3 |
| 1 | ||||
|
| 5 |
| 4 |
(1)请你用含n(n为正整数)的关系式表示上述各式子的变形规律.并证明你的结论.
(2)利用上面的结论,求下列式子的值:(
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 2008 |
分析:(1)本题是一道规律题,很容易发现相邻的两个实数的和倒数就是这两个相邻实数的差.从而求出其值.
(2)利用(1)的结论进行化简,然后运用平方差公式计算就可以了.
(2)利用(1)的结论进行化简,然后运用平方差公式计算就可以了.
解答:解:(1)∵
=
-1,
=
-
,
=
-
,
=
-
…
∴第n的一个式子可以表示为:
=
-
(n≥1的整数).
证明:∵
=
=
=
-
.
∴
=
-
(n≥1的整数).
(2)原式=[(
-1)+(
-
)+(
-
)+…+(
-
)](
+1)
=[
-1+
-
+
-
+…+
-
](
+1)
=[
-1](
+1)
=2007.
| 1 | ||
|
| 2 |
| 1 | ||||
|
| 3 |
| 2 |
| 1 | ||||
|
| 4 |
| 3 |
| 1 | ||||
|
| 5 |
| 4 |
∴第n的一个式子可以表示为:
| 1 | ||||
|
| n+1 |
| n |
证明:∵
| 1 | ||||
|
| ||||||||
(
|
=
| ||||
| n+1-n |
=
| n+1 |
| n |
∴
| 1 | ||||
|
| n+1 |
| n |
(2)原式=[(
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2008 |
| 2007 |
| 2008 |
=[
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2008 |
| 2007 |
| 2008 |
=[
| 2008 |
| 2008 |
=2007.
点评:本题考查分母有理化的运用,平方差公式的运用,在解答中注意观察题目的变化规律,运用规律解答能使运算简便,并且得心应手.

练习册系列答案
相关题目
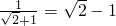 ,
,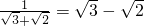 ,
,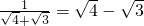 ,
,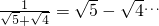
 .
.