题目内容

观察下列一组式的变形过程，然后回答问题：
例1：
1
2
+1
=
2
-1
(
2
+1)(
2
-1)
=
2
-1
(
2
)2-1
=
2
-1
1
=
2
-1，
例2：
1
3
+
2
=
3
-
2
，
1
4
+
3
=
4
-
3
，
1
5
+
4
=
5
-
4
…
（1）
1
6
+
5
=
6
-
5
6
-
5
；
1
2010
+
2009
=
2010
-
2009
2010
-
2009
．
（2）请你用含n（n为正整数）的关系式表示上述各式子的变形规律．
（3）利用上面的结论，求下列式子的值．
1
2
+1
+
1
3
+
2
+
1
4
+
3
+…+
1
2010
+
2009
．
分析：（1）将
1
6
+
5
，
1
2010
+
2009
分母有理化，有理化因式分别为
6
-
5
，
2010
-
2009
；
（2）
1
n+1
+
n
=
n+1
-
n
；
（3）由（1）（2）得，原式═
2
-1+
3
-
2
+
4
-
3
+…+
2010
-
2009
，合并可得结果．
解答：解：（1）
6
-
5
；
2010
-
2009
；

（2）
1
n+1
+
n
=
n+1
-
n
；

（3）原式=
2
-1+
3
-
2
+
4
-
3
+…+
2010
-
2009

=
2010
-1．
故答案为
6
-
5
；
2010
-
2009
．
点评：本题考查分母有理化，找规律是解决此题的关键．
练习册系列答案
相关题目
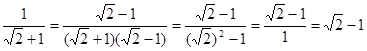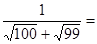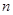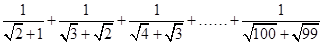
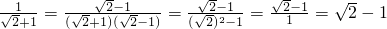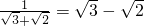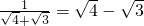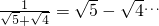
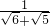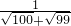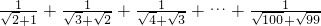观察下列一组式的变形过程，然后回答问题：
例1：
1
2
+1
=
2
-1
(
2
+1)(
2
-1)
=
2
-1
(
2
)2-1
=
2
-1
1
=
2
-1，
例2：
1
3
+
2
=
3
-
2
，
1
4
+
3
=
4
-
3
，
1
5
+
4
=
5
-
4
…
（1）
1
6
+
5
=
 
；
1
100
+
99
=
 

（2）请你用含n（n为正整数）的关系式表示上述各式子的变形规律．
（3）利用上面的结论，求下列式子的值．
1
2
+1
+
1
3
+
2
+
1
4
+
3
+…+
1
100
+
99
．

观察下列一组式的变形过程，然后回答问题：
例1： ，
例2： ，，
利用以上结论解答以下问题：（不必证明）
（1）                  ；                ；
（2）请你用含（为正整数）的关系式表示上述各式子的变形规律。
（3）利用上面的结论，求下列式子的值。（有过程）

观察下列一组式的变形过程，然后回答问题：

例1： ，

例2： ，，

利用以上结论解答以下问题：（不必证明）

（1）                  ；                ；

（2）请你用含（为正整数）的关系式表示上述各式子的变形规律。

（3）利用上面的结论，求下列式子的值。（有过程）

 

观察下列一组式的变形过程，然后回答问题：
例1：数学公式，
例2：数学公式，数学公式，数学公式
（1）数学公式=______；数学公式=______
（2）请你用含n（n为正整数）的关系式表示上述各式子的变形规律．
（3）利用上面的结论，求下列式子的值．数学公式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网