Question

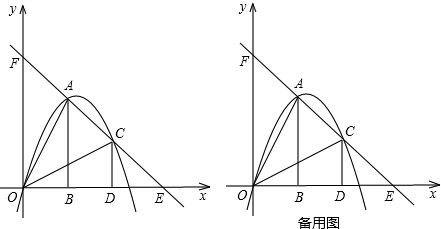
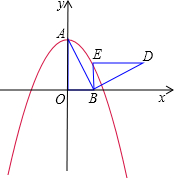
已知：直角梯形AOBC在平面直角坐标系中的位置如图，若AC∥OB，OC平分∠AOB，CB⊥x轴于B，点A坐标为(3 ，4). 点P从原点O开始以2个单位/秒速度沿x轴正向运动 ；同时，一条平行于x轴的直线从AC开始以1个单位/秒速度竖直向下运动 ，交OA于点D，交OC于点M，交BC于点E. 当点P到达点B时，直线也随即停止运动.

（1）求出点C的坐标；

（2）在这一运动过程中, 四边形OPEM是什么四边形？请说明理由。若

用y表示四边形OPEM的面积 ，直接写出y关于t的函数关系式及t的

范围；并求出当四边形OPEM的面积y的最大值？

（3）在整个运动过程中，是否存在某个t值，使⊿MPB为等腰三角形？

若有，请求出所有满足要求的t值.

 

Answer 1

【答案】

（1）点C的坐标是（8，5）（2）四边形OPEM是平行四边形，理由见解析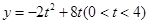；，y=8

（3）

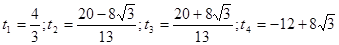
【解析】（1）点C的坐标是（8，5）；

    （2）四边形OPEM是平行四边形.理由：

由题意：OP=2t，

由OC平分∠AOB，AC∥OB，易得：

DM=OD，

延长CA与y轴相交于点L，过点D作

AC的垂线，交AC于H，交OB于K.

则⊿ADH∽⊿ODK∽⊿AOL，

由题意：DH=t,DK=4-t，

DM=OD=5-5/4t，AH=3/4t，DE=HC=5+3/4t,

∴ME=DE-DM=（5+3/4t）-（5-5/4t）=2t，

∴ME=OP，且ME∥OP，∴四边形OPEM是平行四边形;

平行四边形OPEM的面积：

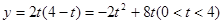
当t=2时，OPEM面积最大值：y=8.

（3）分类讨论如下：

ⅰ：若PM=BM，由题意：BR=ME=2t，

   PR=OB-BR-OP=8-4t，

 此时PR=BR，即2t=8-4t，t=4/3；

ⅱ：若PM=PB，由题意：PB=8-2t，

   PM=8-2t，MR=4－t，PR=8-4t，

在RT⊿PMR中，

解得：

都符合题意；

 

ⅲ：若BM=BP，由题意：PB=8-2t，

   BR=ME=2t，MR=BE=4-t，

在RT⊿BMR中，

  

∴符合题意的t值共四个：

本试题主要是考查了点的坐标的求解，以及四边形形状的确定和四边形的面积的求解的综合运用。同时要分析得到使⊿MPB为等腰三角形的参数t的值。关键是基于对点的运动的理解和表示

	A