题目内容
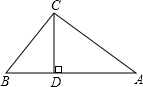如图，在△ABC中，∠ACB=90°，BC=4，AC=5，CD⊥AB，则sin∠ACD的值是分析：在△ABC中，∠ACB=90°，BC=4，AC=5，根据勾股定理就可以求出AB的长，易证Rt△ABC∽Rt△ACD，则就可以把求sin∠ACD与求tan∠BCD的值的问题转化为求直角△ABC的边的比的问题．
解答：解：∵△ABC中，∠ACB=90°，BC=4，AC=5，CD⊥AB，
∴AB=
=
=
．
在Rt△ABC与Rt△ACD中，∠A+∠B=90°，∠A+∠ACD=90°∠ADC=∠ACB=90°．
∴∠B=∠ACD．Rt△ABC∽Rt△ACD，∠BCD=∠A．
故sin∠ACD=sin∠B=
=
=
，tan∠BCD=tan∠A=
=
．
∴AB=
| AC2+BC2 |
| 52+42 |
| 41 |
在Rt△ABC与Rt△ACD中，∠A+∠B=90°，∠A+∠ACD=90°∠ADC=∠ACB=90°．
∴∠B=∠ACD．Rt△ABC∽Rt△ACD，∠BCD=∠A．
故sin∠ACD=sin∠B=
| AC |
| AB |
| 5 | ||
|
5
| ||
| 41 |
| BC |
| AC |
| 4 |
| 5 |
点评：三角函数值只与角的大小有关，因而求一个角的函数值，可以转化为求与它相等的其它角的三角函数值．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
相关题目
20、如图，在△ABC中，∠BAC=45°，现将△ABC绕点A逆时针旋转30°至△ADE的位置，使AC⊥DE，则∠B=
如图，在△ABC中，∠ACB=90°，AC=BC=1，取斜边的中点，向斜边作垂线，画出一个新的等腰三角形，如此继续下去，直到所画出的直角三角形的斜边与△ABC的BC重叠，这时这个三角形的斜边为
2、如图，在△ABC中，DE∥BC，那么图中与∠1相等的角是（ ）
如图，在△ABC中，AB=AC，且∠A=100°，∠B=