题目内容
函数y=x+m与y=
（m≠0）在同一坐标系内的图象可以是（ ）
| m |
| x |
A、 |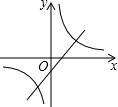
B、 |
C、 |
D、 |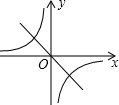
分析：先根据一次函数的性质判断出m取值，再根据反比例函数的性质判断出m的取值，二者一致的即为正确答案．
解答：解：A、由函数y=x+m的图象可知m＜0，由函数y=
的图象可知m＞0，相矛盾，故错误；
B、由函数y=x+m的图象可知m＞0，由函数y=
的图象可知m＞0，正确；
C、由函数y=x+m的图象可知m＞0，由函数y=
的图象可知m＜0，相矛盾，故错误；
D、由函数y=x+m的图象可知m=0，由函数y=
的图象可知m＜0，相矛盾，故错误．
故选B．
| m |
| x |
B、由函数y=x+m的图象可知m＞0，由函数y=
| m |
| x |
C、由函数y=x+m的图象可知m＞0，由函数y=
| m |
| x |
D、由函数y=x+m的图象可知m=0，由函数y=
| m |
| x |
故选B．
点评：本题主要考查了反比例函数的图象性质和一次函数的图象性质，要掌握它们的性质才能灵活解题．
练习册系列答案
相关题目
函数y=ax-a与y=
（a≠0）在同一直角坐标系中的图象可能是（ ）
| a |
| x |
A、 |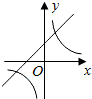
B、 |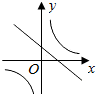
C、 |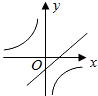
D、 |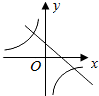
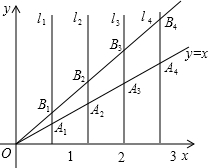（2012•峨边县模拟）如图，直线l1、l2、l3…ln同垂直于x轴，垂足依次为（1，0）（2，0）（3，0）（4，0）…（n，0）函数y=x分别相交于A1、A2、A3…A；函数y=2x分别与直线 l1、l2、l3…ln相交于B1、B2、B3…Bn，如果△A1OB1的面积为S1，四边形A1A2B2B1的面积记为S2，四边形A2A3B3B2的面积记为S3…，四边形An-1AnBnBn-1的面积记为Sn，那么S1=
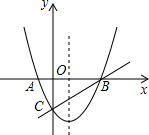如图在同一直角坐标系中，二次函数的图象与两坐标轴分别交于点A（-1，0）、点B（3，0）和点C（0，-3）一次函数的图象与抛物线交于B，C两点
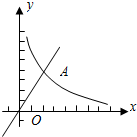已知图中的曲线是反比例函数