题目内容
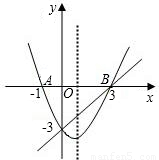
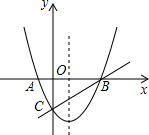 如图在同一直角坐标系中,二次函数的图象与两坐标轴分别交于点A(-1,0)、点B(3,0)和点C(0,-3)一次函数的图象与抛物线交于B,C两点
如图在同一直角坐标系中,二次函数的图象与两坐标轴分别交于点A(-1,0)、点B(3,0)和点C(0,-3)一次函数的图象与抛物线交于B,C两点(1)求二次函数的表达式;
(2)当x取什么值时,两个函数的函数值都随x增大而增大?
(3)当x取什么值时,一次函数值大于二次函数值?
分析:(1)先根据题意,将A(-1,0)、点B(3,0)和点C(0,-3)代入二次函数的解析式,求得a、b、c的值,然后将其代入抛物线y=ax2+bx+c,从而求得二次函数的解析式;
(2)求得函数的对称轴,根据二次函数的性质即可求解;
(3)根据函数的图象,一次函数值大于二次函数值即对于相同的x的值,一次函数对应的图象在上边,即可直接写出x的范围.
(2)求得函数的对称轴,根据二次函数的性质即可求解;
(3)根据函数的图象,一次函数值大于二次函数值即对于相同的x的值,一次函数对应的图象在上边,即可直接写出x的范围.
解答:解:(1)根据题意,知
,
解得,
,
故二次函数的表达式是:y=x2-2x-3;
(2)抛物线的对称轴是:x=1,则当x>1时,两个函数的函数值都随x增大而增大;
(3)根据图象可得0<x<3时,一次函数值大于二次函数值.
|
解得,
|
故二次函数的表达式是:y=x2-2x-3;
(2)抛物线的对称轴是:x=1,则当x>1时,两个函数的函数值都随x增大而增大;
(3)根据图象可得0<x<3时,一次函数值大于二次函数值.
点评:本题考查了待定系数法求函数的解析式,以及二次函数的性质,正确根据函数的图象比较函数值的大小是关键.

练习册系列答案
相关题目
 24、如图在同一直角坐标系中,抛物线与两坐标轴分别交A(-1,0)、B(3,0)和C(0,-3),一次函数的图象与抛物线交于B、C两点.
24、如图在同一直角坐标系中,抛物线与两坐标轴分别交A(-1,0)、B(3,0)和C(0,-3),一次函数的图象与抛物线交于B、C两点.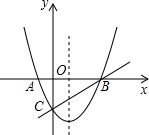 如图在同一直角坐标系中,二次函数的图象与两坐标轴分别交于点A(-1,0)、点B(3,0)和点C(0,-3)一次函数的图象与抛物线交于B,C两点
如图在同一直角坐标系中,二次函数的图象与两坐标轴分别交于点A(-1,0)、点B(3,0)和点C(0,-3)一次函数的图象与抛物线交于B,C两点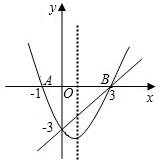 ,一次函数的图象与抛物线交于B、C两点.
,一次函数的图象与抛物线交于B、C两点.