题目内容
【题目】如图，在△ABC中，AD平分∠BAC，CD⊥AD于点D，∠DCB=∠B．若AC=10，AB=25，求CD的长．
【答案】7.5
【解析】延长CD交AB于点E，构建全等三角形：△ADE≌△ADC（ASA）．由全等三角形的对应边相等推知AE＝AC＝10，DE＝DC；根据BE＝CE，AB＝25，得出AB＝AE＋BE＝10＋2DC＝25，即可求得DC＝7.5．
如图，延长CD交AB于点E．
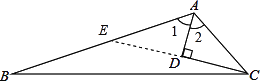
∵AD平分∠BAC，
∴∠1=∠2．
∵CD⊥AD，
∴∠ADE=∠ADC=90°．
∵在△ADE与△ADC中，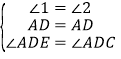
，
∴△ADE≌△ADC（ASA）．
∴AE=AC=10，DE=DC．
∵∠DCB=∠B，
∴BE=CE=2DC．
∴AB=AE+BE=10+2DC=25．
∴DC=7.5．
练习册系列答案
阅读快车系列答案
相关题目
