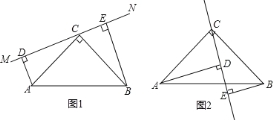
��Ŀ����
����Ŀ������������ֱ��������2��1��-3��-4�IJ�����Ƭ�����dz�����������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ�����ſ�Ƭ���������ȡһ�Ų��Żأ����ÿ�Ƭ�ϵ����ּ�Ϊm�����������ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊn��
��1���뻭����״ͼ��д����m��n�����п��ܵĽ����
��2������ѡ����m��n��ʹһ�κ���y=mx+n��ͼ���ڶ������������ĸ��ʣ�
���𰸡���1�����п��ܵĽ������������2��![]() ��
��
��������
�����������1�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����
��2�����ȿɵ���ѡ����m��n��ʹһ�κ���y=mx+n��ͼ���ڶ��������������У���-3��-4������-4��-3���������ø��ʹ�ʽ������ô𰸣�
�����������1������״ͼ�ã�
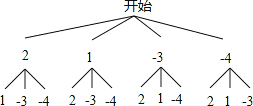
��m��n������12�ֵȿ��ܵĽ������2��1������2��-3������2��-4������1��2������1��-3������1��-4������-3��2������-3��1������-3��-4������-4��2������-4��1������-4��-3����
��2������ѡ����m��n��ʹһ�κ���y=mx+n��ͼ���ڶ������������У���-3��-4������-4��-3����
����ѡ����m��n��ʹһ�κ���y=mx+n��ͼ���ڶ����������ĸ���Ϊ��![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ�����������±�������ʾij���е�ƽ��ʾ��ͼ���������C��3����ʾ��������Ʒ����λ�ã���ô��ʾ����ͯ��װ����λ��Ӧ������ ��
A | B | C | D | |
1 | ����̨ | ����̨ | ����̨ | ����̨ |
2 | ��ˮ | �ǹ� | СʳƷ | ��ʳ |
3 | ��ͯ��װ | ��ױƷ | ������Ʒ | �߲� |
4 | ��� | ��װ | �ҵ� | ������Ʒ |
A. ��A��3�� B. ��B��4�� C. ��C��2�� D. ��D��1��