题目内容
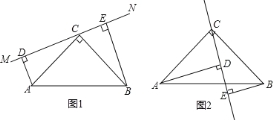
【题目】如图(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)求证: DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?请直接写出你的结论,不必说明理由.
【答案】(1)证明见解析;(2)DE=AD-BE
【解析】
试题分析:(1)、根据三垂直得出∠ACD=∠CBE,然后得出△ADC和△CEB全等,从而得出AD=CE,DC=BE,从而得到结论;(2)、首先证明△ADC和△CEB全等,从而得出AD=CE,DC=BE,得出结论.
试题解析:(1)、∵∠ACB=90°, ∴∠ACD+∠BCE=90°, 而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°, ∴∠ACD=∠CBE.
在△ADC和△CEB中,∠ADC=∠CBE,∠ACD=∠CBE,AC=BC ∴△ADC≌△CEB,
∴AD=CE,DC=BE, ∴DE=DC+CE=BE+AD;
(2)、在△ADC和△CEB中,∠ADC=∠CBE=90°,∠ACD=∠CBE,AC=CB ∴△ADC≌△CEB,
∴AD=CE,DC=BE, ∴DE=CE-CD=AD-BE;

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目