题目内容
设m和n是方程x2+x-2012=0的两个实数根,则m2-n的值为
2013
2013
.分析:先根据一元二次方程的解的定义得到m2+m-2012=0,变形有m2=2012-m,则m2-n=2012-m-n=2012-(m+n),再根据根与系数的关系得到m+n=-1,然后利用整体思想进行计算.
解答:解:∵m是方程x2+x-2012=0的根,
∴m2+m-2012=0,
∴m2=2012-m,
∴m2-n=2012-m-n=2012-(m+n),
∵m和n是方程x2+x-2012=0的两个实数根,
∴m+n=-1,
∴m2-n=2012-(-1)=2013.
故答案为2013.
∴m2+m-2012=0,
∴m2=2012-m,
∴m2-n=2012-m-n=2012-(m+n),
∵m和n是方程x2+x-2012=0的两个实数根,
∴m+n=-1,
∴m2-n=2012-(-1)=2013.
故答案为2013.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为为x1,x2,则x1+x2=-
,x1•x2=
.也考查了一元二次方程的解.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目

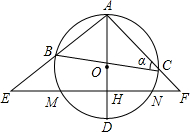 na=
na= ,EH-HF=2.设∠ACB=a,tana=
,EH-HF=2.设∠ACB=a,tana= ,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.
,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.