题目内容
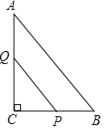
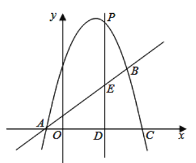
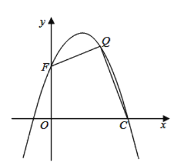
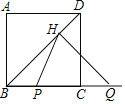
【题目】如图,正方形ABCD的边长为2,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为( )
A.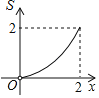 B.
B.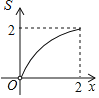
C.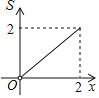 D.
D.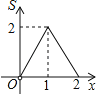
【答案】A
【解析】
过点H作HE⊥BC,垂足为E,易得△BHQ为等腰直角三角形,进而得到HE=![]() BQ=
BQ=![]() ,再利用三角形面积公式表示出△BPH的面积,建立S与x之间的函数关系式,即可判断图像.
,再利用三角形面积公式表示出△BPH的面积,建立S与x之间的函数关系式,即可判断图像.
解:过点H作HE⊥BC,垂足为E,如图,
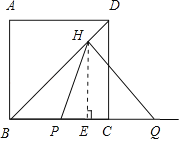
∵BD是正方形的对角线
∴∠DBC=45°
∵QH⊥BD
∴△BHQ是等腰直角三角形
又∵HE⊥BQ
∴E为BQ边上的中点,即HE为斜边BQ上的中线
∴HE=![]() BQ=
BQ=![]()
∴△BPH的面积S=![]() BPHE=
BPHE=![]()
![]() =
=![]()
∴S与x之间的函数关系是二次函数,且二次函数图象开口方向向上;
因此,选项中只有A选项符合条件.
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目