题目内容
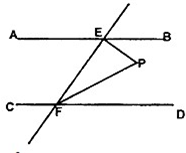 21、如图,若AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,则∠EPF=
21、如图,若AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,则∠EPF=65
度.分析:由题可直接求得∠BEF,然后根据两直线平行,同旁内角互补可知∠DFE,根据角平分线的性质可求得∠EFP,最后根据三角形内角和求出∠EPF.
解答:解:∵EP⊥EF,
∴∠PEF=90°,
∵∠BEP=40°,
∴∠BEF=∠PEF+∠BEP=130°,
∵AB∥CD,
∴∠EFD=180°-∠BEF=50°,
∵FP平分∠EFD,
∴∠EFP=0.5×∠EFD=25°,
∴∠P=180°-∠PEF-∠EFP=65°.
∴∠PEF=90°,
∵∠BEP=40°,
∴∠BEF=∠PEF+∠BEP=130°,
∵AB∥CD,
∴∠EFD=180°-∠BEF=50°,
∵FP平分∠EFD,
∴∠EFP=0.5×∠EFD=25°,
∴∠P=180°-∠PEF-∠EFP=65°.
点评:本题用到的知识点为:三角形的内角和是180°,以及平行线的性质:两直线平行,同旁内角互补.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
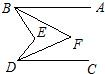 如图,若AB∥CD,∠ABE和∠CDE的平分线交于点F,且∠BED=75°,那么∠BFD等于( )
如图,若AB∥CD,∠ABE和∠CDE的平分线交于点F,且∠BED=75°,那么∠BFD等于( )| A、35° | B、37.5° | C、38.5° | D、36° |
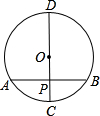 垂直于弦的直径平分这条弦,并且平弦所对的弧.
垂直于弦的直径平分这条弦,并且平弦所对的弧.
 如图,若AB∥CD,EF与AB、CD分别相交于E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,求∠P的度数.
如图,若AB∥CD,EF与AB、CD分别相交于E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,求∠P的度数.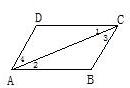 6、如图,若AB∥CD,则①∠1=∠2;②∠3=∠4;③∠1+∠3=∠2+∠4,上述结论正确的是( )
6、如图,若AB∥CD,则①∠1=∠2;②∠3=∠4;③∠1+∠3=∠2+∠4,上述结论正确的是( )