题目内容
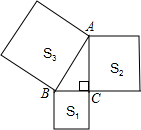如图，以Rt△ABC的三边为边向外作正方形，其面积分别为S1，S2，S3，且S1=4，S2=9，则AB的长=| 13 |
| 13 |
分析：先利用正方形的面积公式分别求出正方形S1、S2的边长即BC、AC的长，在Rt△ABC中，已知AC、BC的长，利用勾股定理求斜边AB．
解答：解：∵S1=4，
∴BC2=4，
∵S2=9，
∴AC2=9，
∵在Rt△ABC中，BC2+AC2=AB2，
∴AB=
=
，
故答案为：
．
∴BC2=4，
∵S2=9，
∴AC2=9，
∵在Rt△ABC中，BC2+AC2=AB2，
∴AB=
| 9+4 |
| 13 |
故答案为：
| 13 |
点评：此题主要考查了正方形的面积公式及勾股定理的应用，关键是熟练掌握勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
练习册系列答案
相关题目
23、如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接ED、BD．
如图，以Rt△ABC各边为直径的三个半圆围成两个新月形（阴影部分），已知AC=3cm，BC=4cm．则新月形（阴影部分）的面积和是
已知，如图，以Rt△ABC的斜边AB为直径作⊙0，D是BC上的点，且有弧AC=弧CD，连CD、BD，在BD延长线上取一点E，使∠DCE=∠CBD．
如图，以Rt△ABC的直角边AC为直径作圆O交斜边AB于点D，若劣弧CD=120°，则
（2009•黔南州）如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接DE．