题目内容
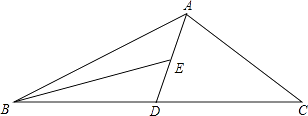
【题目】如图，AD为△ABC的中线，BE为三角形ABD中线．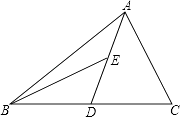 
（1）在△BED中作BD边上的高EF；
（2）若△ABC的面积为40，BD=5，求EF的长．
【答案】
（1）解；如图所示：
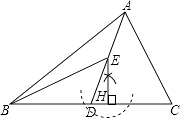
（2）解；∵AD为△ABC的中线，BE为三角形ABD中线，
∴S△ABD= 
S△ABC，S△BDE= S△ABD，
∴S△BDE= 
S△ABC，
∵△ABC的面积为40，BD=5，
∴ ×5×EF=10，
∴EF=4
【解析】（1）根据过直线外一点作已知直线的垂线的方法作图即可；（2）利用三角形中线的性质得出S△BDE= S△ABC ， 进而借助三角形面积公式求出即可．
【考点精析】掌握三角形的面积是解答本题的根本，需要知道三角形的面积=1/2×底×高．
练习册系列答案
相关题目
【题目】某校食堂的中餐与晚餐的资费标准如下：
种类 | 单价 |
米饭 | 0.5元/份 |
A类套餐菜 | 3.5元/份 |
B类套餐菜 | 2.5元/份 |
小杰同学某星期从周一到周五每天的中餐与晚餐均在学校选用A类或B类中的一份套餐菜与一份米饭用餐，这五天共消费36元．请问小杰在这五天内，A，B类套餐菜各选用了多少次？
