题目内容
【题目】如图，给定一个半径长为2的圆，圆心O到水平直线l的距离为d，即OM=d．我们把圆上到直线l的距离等于1的点的个数记为m．如d=0时，l为经过圆心O的一条直线，此时圆上有四个到直线l的距离等于1的点，即m=4，由此可知：
①当d=3时，m= ；
②当m=2时，d的取值范围是 ．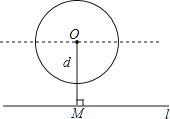
【答案】1；0＜d＜3
【解析】解：①当d=3时，
∵3＞2，即d＞r，
∴直线与圆相离，则m=1，
故答案为：1；
②当m=2时，则圆上到直线l的距离等于1的点的个数记为2，
∴直线与圆相交或相切或相离，
∴0＜d＜3，
∴d的取值范围是0＜d＜3，
故答案为：0＜d＜3．
根据直线与圆的位置关系和直线与圆的交点个数以及命题中的数据分析即可得到答案．本题考查了直线与圆的位置关系，解题的关键是了解直线与圆的位置关系与d与r的数量关系．
互动课堂系列答案
激活思维智能训练课时导学练系列答案
【题目】华联超市用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的
多15件，甲、乙两种商品的进价和售价如下表：（注：获利＝售价﹣进价）
甲 | 乙 | |
进价（元/件） | 22 | 30 |
售价（元/件） | 29 | 40 |
（1）该商场购进甲、乙两种商品各多少件？
（2）该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润？
【题目】在2016CCTV英语风采大赛中，娄底市参赛选手表现突出，成绩均不低于60分．为了更好地了解娄底赛区的成绩分布情况，随机抽取利了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行了整理，得到如图的两幅不完整的统计图表：
根据所给信息，解答下列问题：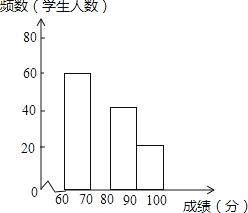
（1）在表中的频数分布表中，m= ， n= ．
成绩 | 频数 | 频率 |
60≤x＜70 | 60 | 0.30 |
70≤x＜80 | m | 0.40 |
80≤x＜90 | 40 | n |
90≤x≤100 | 20 | 0.10 |
（2）请补全图中的频数分布直方图．
（3）按规定，成绩在80分以上（包括80分）的选手进入决赛．若娄底市共有4000人参数，请估计约有多少人进入决赛？
