题目内容
 (2013•龙湾区一模)如图,热气球从山顶A竖直上升至点B需25秒,点D在地面上,DC⊥AB,垂足为C,从地面上点D分别仰视A,B两点,测得∠ADC=20°,∠BDC=60°,若CD=130米.求该热气球从山顶A竖直上升至点B的平均速度.(结果精确到0.1米/秒)
(2013•龙湾区一模)如图,热气球从山顶A竖直上升至点B需25秒,点D在地面上,DC⊥AB,垂足为C,从地面上点D分别仰视A,B两点,测得∠ADC=20°,∠BDC=60°,若CD=130米.求该热气球从山顶A竖直上升至点B的平均速度.(结果精确到0.1米/秒)(参考数据:tan20°≈0.36,tan30°=0.58,tan60°≈1.73,tan70°≈2.75)
分析:在Rt△ADC中求出AC,在Rt△BDC中求出BC,继而得出AB的长度,再由热气球从山顶A竖直上升至点B需25秒,可得出热气球的平均速度.
解答:解:在Rt△ADC中,∠ADC=20°,CD=130米,
则AC=CDtan∠ADC=CDtan20°=46.8米,
在Rt△BDC中,∠BDC=60°,CD=130米,
则BC=CDtan∠BDC=CDtan60°=224.9米,
故AB=BC-AC=178.1米,
该热气球从山顶A竖直上升至点B的平均速度设该热气球从山顶A竖直上升至点B的平均速度=
≈7.1米/秒.
答:该热气球从山顶A竖直上升至点B的平均速度设该热气球从山顶A竖直上升至点B的平均速度7.1米/秒
则AC=CDtan∠ADC=CDtan20°=46.8米,
在Rt△BDC中,∠BDC=60°,CD=130米,
则BC=CDtan∠BDC=CDtan60°=224.9米,
故AB=BC-AC=178.1米,
该热气球从山顶A竖直上升至点B的平均速度设该热气球从山顶A竖直上升至点B的平均速度=
| 178.1 |
| 25 |
答:该热气球从山顶A竖直上升至点B的平均速度设该热气球从山顶A竖直上升至点B的平均速度7.1米/秒
点评:本题考查了解直角三角形的应用,解答本题需要我们能利用三角函数值及已知线段求出直角三角形中的其他线段,难度一般.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
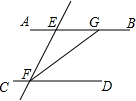 (2013•龙湾区一模)如图,已知AB∥CD,直线EF分别交AB,CD于点 E,F,FG平分∠EFD交AB于点G,若∠EFD=70°,则∠EGF的度数是( )
(2013•龙湾区一模)如图,已知AB∥CD,直线EF分别交AB,CD于点 E,F,FG平分∠EFD交AB于点G,若∠EFD=70°,则∠EGF的度数是( ) (2013•龙湾区一模)如图,△DEF是由△ABC通过平移得到,且点B,E,C,F在同一条直线上.若BF=14,EC=6.则BE的长度是( )
(2013•龙湾区一模)如图,△DEF是由△ABC通过平移得到,且点B,E,C,F在同一条直线上.若BF=14,EC=6.则BE的长度是( ) (2013•龙湾区一模)二次函数
(2013•龙湾区一模)二次函数