Question

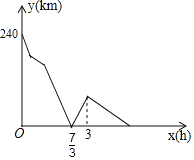
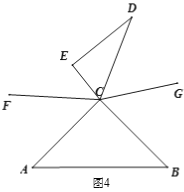
【题目】已知将一副三角板(直角三角板ABC和直角三角板CDE，∠ACB＝90°，∠ECD＝60°)如图1摆放，点D、A、C在一条直线上，将直角三角板CDE绕点C逆时针方向转动，变化摆放如图位置.

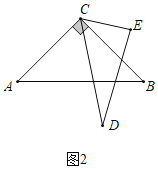
(1) 如图2，当∠ACD为多少度时，CB恰好平分∠ECD？

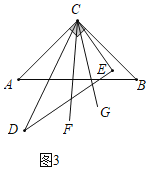
(2) 如图3，当三角板CDE摆放在∠ACB内部时，作射线CF平分∠ACE，射线CG平分∠BCD，如果三角形CDE在∠ACB内绕点C任意转动，∠FCG的度数是否发生变化？如果不变，求其值；如果变化，说明理由.

(3) 如图4，当三角板CDE转到∠ACB外部时，射线CF、CG仍然分别平分∠ACE、∠BCD，在旋转过程中，(2)中的结论是否成立？如果结论成立，请说明理由；如果不成立，请写出你的结论并根据图4说明理由.

Answer 1

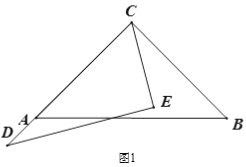
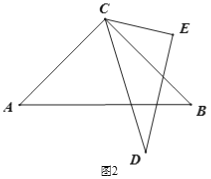
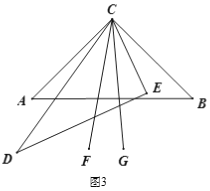
【答案】(1)∠ACD＝60°；(2)不变，∠FCG＝15°；(3)不成立，∠FCG＝165°．

【解析】

（1）由图2可得角之间的关系：∠ACD=∠ACB-∠BCD，所以利用角平分线的定义求出∠BCD的度数即可；

（2）先根据角的和与差得：∠ACD+∠BCE=90°-60°=30°，由图3可得角之间的关系：∠FCG=∠BCF-∠BCG=∠FCE+∠BCE-∠BCG，于是得到结论；

（3）结论：在旋转的过程中，（2）中的结论不成立，同理根据（2）可得结论．

解：（1）在图2中，∵CB平分∠DCE，

∴∠BCD=∠DCE=×60°=30°，

∴∠ACD=∠ACB-∠BCD=90°-30°=60°；

（2）∠FCG不变，∠FCG=15°，

理由是：如图3，

∵∠ACB=90°，∠DCE=60°，

∴∠ACD+∠BCE=90°-60°=30°，

∵射线CF平分∠ACE，射线CG平分∠BCD，

∴∠FCE=∠ACE=(90°∠BCE)=45°-∠BCE，

∠BCG=∠BCD=(90°∠ACD)=45°-∠ACD，

∴∠FCG=∠BCF-∠BCG=∠FCE+∠BCE-∠BCG=45°-∠BCE+∠BCE-45°+∠ACD=(∠BCE+∠ACD)=15°；

（3）结论：在旋转的过程中，（2）中的结论不成立．

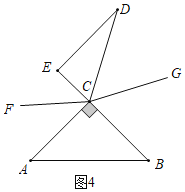
理由：∵∠ACB=90°，∠DCE=60°，

∴∠ACE+∠BCD=360°-90°-60°=210°，

∵射线CF平分∠ACE，射线CG平分∠BCD，

∴∠FCE=∠ACE，∠DCG=∠BCD，

∴∠FCE+∠DCG=×210°=105°，

∴∠FCG=∠FCE+∠DCE+∠DCG=105°+60°=165°．