题目内容
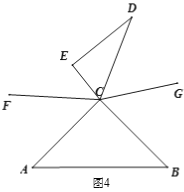
【题目】如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东56°,射线 OC在∠NOE内,且∠NOC与∠BOS互余,射线OA平分∠BON,图中与∠COA互余的角是________.

【答案】∠AON和∠AOB
【解析】
根据方位角的定义及角平分线的定义、余角的概念分别求出∠BOS、∠NOC、∠NOA、∠AOB的度数可得答案.
解:∵∠BOS=56°、∠NOC与∠BOS互余,
∴∠NOC=34°,∠BON=124°,
又∵OA平分∠BON,
∴∠NOA=∠AOB=62°,
则∠AOC=∠NOA-∠NOC=28°,
∵∠NOE=90°、∠NOC=34°,
∴∠COE=56°,
综上,∠COA+∠NOA=90°;∠COA+∠AOB=90°
∴∠COA互余的角有∠NOA、∠AOB,
故答案为:∠AON和∠AOB.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目