Question

【题目】如图，已知∠A＝90°+x°，∠B＝90°﹣x°，∠CED＝90°，4∠C﹣∠D＝30°，射线EF∥AC．

（1）判断射线EF与BD的位置关系，并说明理由；

（2）求∠C，∠D的度数．

Answer 1

【答案】（1）EF∥BD，见解析；（2）．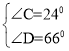

【解析】

（1）由∠A+∠B＝180°，得到AC∥BD，由EF∥AC，得到EF∥BD.

（2）由已知条件得到∠C+∠D＝90°，又因为4∠C﹣∠D＝30°，由两式可得∠C，∠D的度数．

（1）EF∥BD，

∵∠A+∠B＝（90+x）°+（90﹣x）°＝180°，

∴AC∥BD，

∵EF∥AC，

∴EF∥BD；

（2）∵AC∥EF∥BD，

∴∠CEF＝∠C，∠DEF＝∠D，

∵∠CED＝90°，

∴∠C+∠D＝90°，

联立，

解得．