Question

【题目】如图所示，在菱形ABCD中，AB=4，∠BAD=120，△ABF为等边三角形;点E.F分别在菱形的边BC.CD上滑动，且点E.F不与点B.C.D重合，当点E.F分别在BC.CD上滑动时，求四边形ABCF的面积= ___________并求△CEF面积的最大值___________

Answer 1

【答案】

【解析】

①连接AC，证明△ABE≌△ACF，将四边形AECF的面积转化为的面积即可；

②S△CEF=S四边形AECF﹣S△AEF，的面积最小，则可得的面积最大；当正三角形AEF的边AE与BC垂直时，边AE最短，即的面积最小，可得结果．

如图，连接AC，

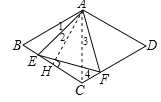
∵四边形ABCD为菱形，

∠BAD=120°，∠1+∠EAC=60°，∠3+∠EAC=60°，

∴∠1=∠3，∵∠BAD=120°，∴∠ABC=60°，

∴△ABC和△ACD为等边三角形，

∴∠4=60°，AC=AB．

在△ABE和△ACF中，

∵∠1=∠3，AC=AC，∠ABC=∠4，

∴△ABE≌△ACF（ASA），

∴S△ABE=S△ACF，

∴S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC，

作AH⊥BC于H点，则BH=2，

∴S四边形AECF=S△ABC=BCAH=BC=，

由“垂线段最短”可知：当正三角形AEF的边AE与BC垂直时，边AE最短，

∴△AEF的面积会随着AE的变化而变化，且当AE最短时，正三角形AEF的面积会最小，

又∵S△CEF=S四边形AECF﹣S△AEF，则此时△CEF的面积就会最大，

∴S△CEF=S四边形AECF﹣S△AEF=﹣×× =．

故答案为.