题目内容
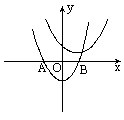
已知：抛物线y＝x2＋bx＋c与x轴交于P，Q两点，与y轴交于点E，且OE＝OP＝PQ．(1)画出抛物线的示意图，并求出抛物线的解析式；(2)问线段EQ上是否存在一点M，使△EMP∽△EPQ？若存在，求出点M的坐标；若不存在，请说明理由．
答案：
解析：
解析：
|
思路点拨：(1)抛物线开口向上，与x轴的两交点P、Q位居y轴的同侧，有两种情况，且P是线段OQ的中点； 由线段相等关系可得方程x2＋bx＋c＝0两根，再用韦达定理列出方程组，并解之得抛物线解析式； (2)假设存在，由相似三角形对应边成比例，列出等式关系，求解得结论． 评注：本题主要考查了抛物线、一元二次方程、直线和相似三角形等知识，同时还考查了方程思想、数形结合思想、分类讨论思想．而第(2)小题又考查了一个存在性探索问题．因此本题思维层次高、运算量大、综合性强，要求考生具有较高的分析问题、探索问题和解决问题的能力． 一般情况下，解决条件探索题时，应先假设结论存在，并在此基础上，结合题设条件进行推理、计算，推出使结论成立的条件或说明不存在使结论成立的条件．由于此类问题的结构都比较复杂，所以往往需要分类讨论． 另外，本题中的两点P、Q会分居原点的两侧吗？事实上是不可能的．若P、Q两点分居原点两侧，则显然有OP＜PQ，这与题设OP＝PQ矛盾．故P、Q两点只能位于原点的同侧． |
练习册系列答案
名校课堂系列答案
相关题目
与抛物线y＝x2＋mx－
m2在平面直角坐标系xOy中的位置如图所示，其中一条与x轴交于A、B两点．
－
＝
，求经过A、B两点的这条抛物线的解析式．
，求抛物线的解析式．”解法的部分步骤如下，补全解题过程，并简述步骤①的解题依据，步骤②的解题方法．
，
．
代入上式，得到关于m的方程
)2＋( ) ②
”改为“△ABC为等边三角形”，用类似的方法求出此抛物线的解析式．