题目内容
已知:抛物线y=x2-mx+![]() 与抛物线y=x2+mx-
与抛物线y=x2+mx-![]() m2在平面直角坐标系xOy中的位置如图所示,其中一条与x轴交于A、B两点.
m2在平面直角坐标系xOy中的位置如图所示,其中一条与x轴交于A、B两点.
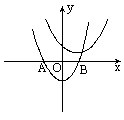
(1)试判断哪条抛物线经过A、B两点,并说明理由;
(2)若A、B两点到原点的距离AO、BO满足![]() -
-![]() =
=![]() ,求经过A、B两点的这条抛物线的解析式.
,求经过A、B两点的这条抛物线的解析式.
答案:
解析:
解析:
|
解:(见答图)
(1)∵抛物线不过原点,∴m≠0. 令x2-mx+ ∵Δ1=(-m)2-4× ∴抛物线y=x2-mx+ 令x2+mx- ∵Δ2=m2-4(- ∴抛物线y=x2+mx- (2)设点A(x1,0),B(x2,0), 则x1,x2为方程x2+mx- ∴x1+x2=-m,x1·x2=- ∵点A在原点的左边,点B在原点的右边, ∴AO=-x1,OB=x2. ∵ ∴ 解得m=2,经检验,m=2是方程的解. ∴所求抛物线的解析式为 y=x2+2x-3. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

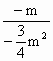 =
=