题目内容
【题目】已知:在平行四边形ABCD 中, A 的角平分线交CD 于 E .
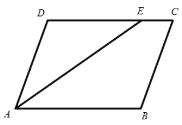
(1)若B 110,求AED 的度数;
(2)若 DE : EC 3 :1, AB 的长为8 ,求 AD 的长.
【答案】(1)AED =35°;(2)AD =6
【解析】
(1)根据平行四边形的性质可得∠DAB的度数,再根据角平分线的定义与平行线的性质即可得解;
(2)根据平行四边形的性质可得CD=AB,然后设CE长x,则DE长3x,求得DE的长,进而得到AD的长.
解:(1)∵四边形ABCD是平行四边形,
∴∠BAD=180°-∠B=70°,
∵AE平分∠BAD,
∴∠BAE=∠DAE=![]() =35°,
=35°,
∵AB∥CD,
∴∠AED=∠BAE=35°;
(2)∵四边形ABCD是平行四边形,
∴CD=AB=8,
设CE长x,则DE长3x,
∴x+3x=8,
解得x=2,
∴DE=3x=6,
∵∠AED=∠DAE,
∴AD=DE=6.

练习册系列答案
相关题目