题目内容
(2012•丰台区二模)如图,将矩形OABC置于平面直角坐标系xOy中,A(2
,0),C(0,2).
(1)抛物线y=-x2+bx+c经过点B、C,求该抛物线的解析式;
(2)将矩形OABC绕原点顺时针旋转一个角度α(0°<α<90°),在旋转过程中,当矩形的顶点落在(1)中的抛物线的对称轴上时,求此时这个顶点的坐标;
(3)如图(2),将矩形OABC绕原点顺时针旋转一个角度θ(0°<θ<180°),将得到矩形OA′B′C′,设A′C′的中点为点E,连接CE,当θ=

| 3 |
(1)抛物线y=-x2+bx+c经过点B、C,求该抛物线的解析式;
(2)将矩形OABC绕原点顺时针旋转一个角度α(0°<α<90°),在旋转过程中,当矩形的顶点落在(1)中的抛物线的对称轴上时,求此时这个顶点的坐标;
(3)如图(2),将矩形OABC绕原点顺时针旋转一个角度θ(0°<θ<180°),将得到矩形OA′B′C′,设A′C′的中点为点E,连接CE,当θ=
120
120
°时,线段CE的长度最大,最大值为4
4
.
分析:(1)首先根据矩形的性质以及A、C点的坐标确定点B的坐标,再利用待定系数法确定该抛物线的解析式.
(2)设抛物线的对称轴与x轴的交点为D,若矩形的顶点恰好落在抛物线对称轴上时,该顶点、O、D正好构成一个直角三角形,由勾股定理即可确定这个顶点的坐标.
(3)观察图示可知:当点E运动到y轴负半轴上时,CE最长,找出了这个关键位置,解答问题就简单多了.
(2)设抛物线的对称轴与x轴的交点为D,若矩形的顶点恰好落在抛物线对称轴上时,该顶点、O、D正好构成一个直角三角形,由勾股定理即可确定这个顶点的坐标.
(3)观察图示可知:当点E运动到y轴负半轴上时,CE最长,找出了这个关键位置,解答问题就简单多了.
解答: 解:(1)∵矩形OABC,A(2
解:(1)∵矩形OABC,A(2
,0),C(0,2),∴B(2
,2).
∴抛物线的对称轴为x=
.∴b=
.
∴二次函数的解析式为:y=-x2+2
x+2.
(2)①当顶点A落在对称轴上时,设点A的对应点为点A′,连接OA′,
设对称轴x=
与x轴交于点D,∴OD=
.
 ∴OA′=OA=2
∴OA′=OA=2
.
在Rt△OA′D中,根据勾股定理A′D=3.
∴A′(
,-3).
②当顶点落C对称轴上时(如图),设点C的对应点为点C′,连接OC′,
在Rt△OC′D中,根据勾股定理C′D=1.
∴C′(
,1).
 (3)如右图,设AC、OB的交点为E;
(3)如右图,设AC、OB的交点为E;
在Rt△OAB中,OA=2
,AB=2,∴∠BOA=30°,OE=AB=2;
在OE旋转过程中,可将点E的轨迹看作是以O为圆心,以OE为半径的圆(旋转角度:0°~180°);
由图可看出,当点E运动到y轴负半轴上时(即点E′的位置),CE最长;
此时,旋转的角度:∠EOE′=∠BOA+90°=30°+90°=120°;
CE的最长值:CE′=OC+OE′=2+2=4;
故填:120°,4.
 解:(1)∵矩形OABC,A(2
解:(1)∵矩形OABC,A(2| 3 |
| 3 |
∴抛物线的对称轴为x=
| 3 |
| 3 |
∴二次函数的解析式为:y=-x2+2
| 3 |
(2)①当顶点A落在对称轴上时,设点A的对应点为点A′,连接OA′,
设对称轴x=
| 3 |
| 3 |
 ∴OA′=OA=2
∴OA′=OA=2| 3 |
在Rt△OA′D中,根据勾股定理A′D=3.
∴A′(
| 3 |
②当顶点落C对称轴上时(如图),设点C的对应点为点C′,连接OC′,
在Rt△OC′D中,根据勾股定理C′D=1.
∴C′(
| 3 |
 (3)如右图,设AC、OB的交点为E;
(3)如右图,设AC、OB的交点为E;在Rt△OAB中,OA=2
| 3 |
在OE旋转过程中,可将点E的轨迹看作是以O为圆心,以OE为半径的圆(旋转角度:0°~180°);
由图可看出,当点E运动到y轴负半轴上时(即点E′的位置),CE最长;
此时,旋转的角度:∠EOE′=∠BOA+90°=30°+90°=120°;
CE的最长值:CE′=OC+OE′=2+2=4;
故填:120°,4.
点评:该题主要考查了函数解析式的确定、矩形的性质、图形的旋转以及勾股定理的应用等综合知识;题目的难度不大,需要注意数形结合思想的应用.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 、第2格、第3格、第4格,这时小正方体朝上一面的字是( )
、第2格、第3格、第4格,这时小正方体朝上一面的字是( )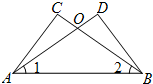 (2012•丰台区二模)如图,在△ABC与△ABD中,BC与AD相交于点O,∠1=∠2,CO=DO.
(2012•丰台区二模)如图,在△ABC与△ABD中,BC与AD相交于点O,∠1=∠2,CO=DO.