题目内容
(2012•丰台区二模)符号“f”表示一种运算,它对一些数的运算如下:f(1)=1+
,f(2)=1+
,f(3)=1+
,f(4)=1+
,…,
利用以上运算的规律写出f(n)=
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| 4 |
利用以上运算的规律写出f(n)=
1+
| 2 |
| n |
1+
(n为正整数);f(1)•f(2)•f(3)…f(100)=| 2 |
| n |
5151
5151
.分析:由已知的一系列等式,归纳总结表示出f(n);由得出的f(n),分别令n=1,2,3,…,100,代入所求式子f(1)•f(2)•f(3)…f(100)中,约分后计算,即可得到结果.
解答:解:由题意总结得:f(n)=1+
;f(n)=
f(1)=
;f(2)=
;f(3)=1+
=
;f(4)=1+
=
;f(5)=1+
=
;
f(6)=1+
=
,…,f(99)=1+
=
,f(100)=1+
=
,
则f(1)•f(2)•f(3)…f(100)=
×
×
×
×…
×
=
=5151.
故答案为:1+
;5151
| 2 |
| n |
| n+2 |
| n |
f(1)=
| 3 |
| 1 |
| 4 |
| 2 |
| 2 |
| 3 |
| 5 |
| 3 |
| 2 |
| 4 |
| 6 |
| 4 |
| 2 |
| 5 |
| 7 |
| 5 |
f(6)=1+
| 2 |
| 6 |
| 8 |
| 6 |
| 2 |
| 99 |
| 101 |
| 99 |
| 2 |
| 100 |
| 102 |
| 100 |
则f(1)•f(2)•f(3)…f(100)=
| 3 |
| 1 |
| 4 |
| 2 |
| 5 |
| 3 |
| 6 |
| 4 |
| 101 |
| 99 |
| 102 |
| 100 |
| 101×102 |
| 1×2 |
故答案为:1+
| 2 |
| n |
点评:此题考查了分式的混合运算,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
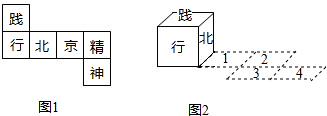 、第2格、第3格、第4格,这时小正方体朝上一面的字是( )
、第2格、第3格、第4格,这时小正方体朝上一面的字是( ) (2012•丰台区二模)如图,在△ABC与△ABD中,BC与AD相交于点O,∠1=∠2,CO=DO.
(2012•丰台区二模)如图,在△ABC与△ABD中,BC与AD相交于点O,∠1=∠2,CO=DO.